Proceso isobárico: fórmulas, ecuaciones, experimentos, ejercicios
En un proceso isobárico, la presión P de un sistema se mantiene constante. El prefijo “iso” proviene del griego y se utiliza para denotar que algo permanece constante, mientras que “baros”, también del griego, significa peso.
Los procesos isobáricos son muy propios tanto en recipientes cerrados como en espacios abiertos, siendo sencillos localizarlos en en la naturaleza. Con ello queremos decir que es posible cambios físicos y químicos en la superficie terrenal o reacciones químicas en recipientes abiertos a la atmósfera.
Algunos ejemplos se obtienen al calentar al sol un globo lleno de aire, cocinar, hervir o congelar agua, el vapor que se genera en las calderas o el proceso de elevar un globo aerostático. Más adelante daremos una explicación de estos casos.
Índice del artículo
Derivemos una ecuación para el proceso isobárico suponiendo que el sistema en estudio es un gas ideal, un modelo bastante adecuado para casi cualquier gas a menos de 3 atmósferas de presión. Las partículas del gas ideal se mueven al azar, ocupan todo el volumen del espacio que las contiene sin interactuar entre sí.
Si al gas ideal encerrado en un cilindro provisto de un pistón movible se le permite expandirse lentamente, se puede suponer que en todo momento sus partículas están en equilibro. Entonces el gas ejerce sobre el pistón de área A una fuerza F de magnitud:
F = p.A
Donde p es la presión del gas. Dicha fuerza ejerce un trabajo produciendo un desplazamiento infinitesimal dx en el pistón dado por:
dW = Fdx = pA.dx
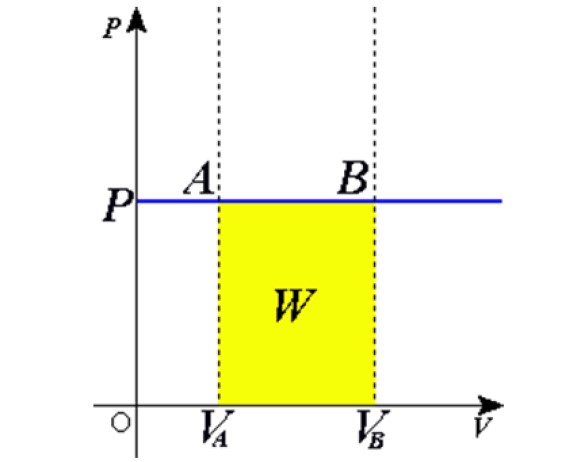
Como el producto Adx es un diferencial de volumen dV, entonces dW = pdV. Resta integrar a ambos lados desde el volumen inicial VA hasta el volumen final VB para obtener el trabajo total realizado por el gas:
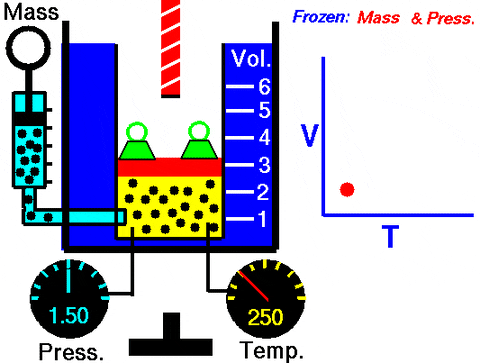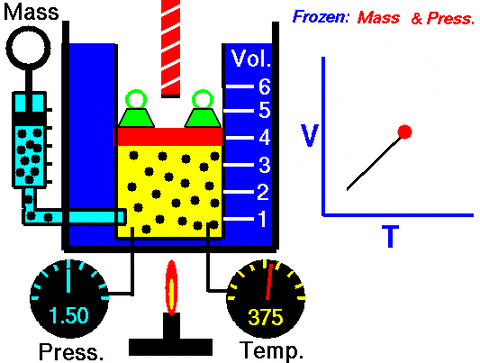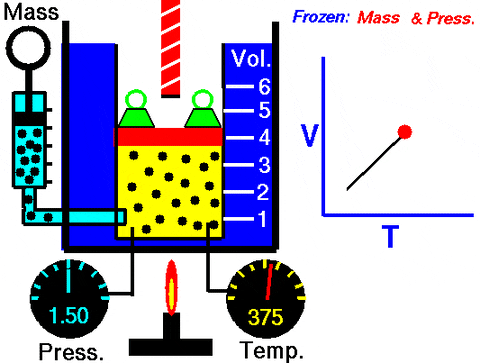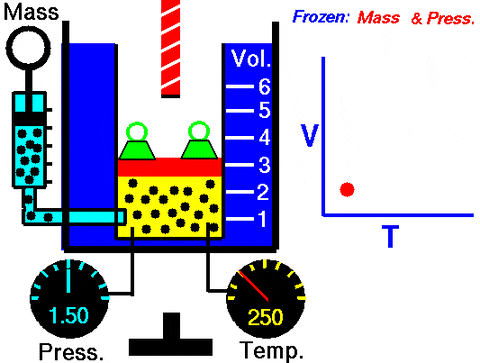
La situación descrita se comprueba experimentalmente confinando un gas dentro de un cilindro provisto de un pistón movible, como se muestra las figuras 2 y 3. Sobre el pistón se coloca una pesa de masa M, cuyo peso se dirige hacia abajo, mientras que el gas ejerce una fuerza hacia arriba gracias a la presión P que produce sobre el pistón.

Ya que el pistón es capaz de moverse libremente, el volumen que ocupa el gas puede cambiar sin problema, pero la presión se mantiene constante. Agregando la presión atmosférica Patm, que también ejerce una fuerza hacia abajo, se tiene:
Mg – P.A + Patm . A = constante
Por lo tanto: P = (Mg/A) + Patm no varía, a menos que se modifique M y con ello el peso. Agregando calor al cilindro, el gas se expandirá aumentando su volumen o bien se contraerá al extraer calor.
La ecuación de estado del gas ideal relaciona las variables de importancia: presión P, volumen V y temperatura T:
P.V= n .R.T
Aquí n representa el número de moles y R es la constante de los gases ideales (válida para todos los gases), que se calcula multiplicando la constante de Boltzmann por el número de Avogadro, dando como resultado:
R = 8.31 J/mol K
Cuando la presión es constante, la ecuación de estado se puede escribir como:
V/T = nR/P
Pero nR/P es constante, ya que n, R y P lo son. Así que cuando el sistema pasa de un estado 1 a otro estado 2, surge la siguiente proporción, conocida también como la ley de Charles:
V1/T1 = V2/T2
Sustituyendo en W = PΔV, se obtiene el trabajo efectuado para ir desde el estado 1 al 2, en términos de las constantes y de la variación de temperatura, fácil de medir con un termómetro:
W1→2 = nR (T2 – T1)=nR.ΔT
Por otro lado, la primera ley de la termodinámica establece que:
∆U = Q – W
Esto significa que añadiendo al gas una cierta cantidad de calor Q, se incrementa la energía interna ∆U y aumentan las vibraciones de sus moléculas. De esta forma, el gas se expande y realiza trabajo desplazando el pistón, como hemos dicho antes.
En un gas ideal monoatómico y la variación de la energía interna ∆U, que incluye tanto la energía cinética como la energía potencial de sus moléculas, es:
∆U = (3/2)nR ΔT
Finalmente combinamos en una sola las expresiones que hemos ido obteniendo:
Q= ∆U + W= (3/2)nR ΔT+ nR ∆T = (5/2) nR ΔT
Alternativamente Q se puede reescribir en términos de la masa m, la diferencia de temperaturas y una nueva constante llamada calor específico del gas a presión constante, abreviadamente cp, cuyas unidades son J/mol K:
Q = m cp ∆T
No todos los procesos isobáricos se llevan a cabo en recipientes cerrados. De hecho ocurren innumerables procesos termodinámicos de todo tipo a presión atmosférica, así que los procesos isobáricos son muy frecuentes en la naturaleza. Esto incluye cambios físicos y químicos en la superficie terrestre, reacciones químicas en recipientes abiertos a la atmósfera y mucho más.
Para que los procesos isobáricos se den en sistemas cerrados, es preciso que las fronteras de los mismos sean los suficientemente flexibles como para permitir los cambios en el volumen sin que varíe la presión.
Esto era lo que sucedía en el experimento del pistón que se desplazaba fácilmente al expandirse el gas. Sucede igual encerrando un gas en un globo para fiestas o un globo aerostático.
Aquí tenemos varios ejemplos de procesos isobáricos:
Poner a hervir agua para el té o cocinar salsas en recipientes abiertos son buenos ejemplos de procesos isobáricos, ya que todos se desarrollan a presión atmosférica.
Al calentar el agua, la temperatura y el volumen aumentan y si se continúa agregando calor se llega finalmente al punto de ebullición, en el cual ocurre el cambio de fase del agua de líquida a vapor de agua. Mientras esto ocurre, la temperatura también se mantiene constante de 100 º C.
Por otra parte, congelar agua también es un proceso isobárico, ya sea que tenga lugar en un lago durante el invierno o el refrigerador doméstico.
Otro ejemplo de proceso isobárico es el cambio en el volumen de un globo inflado con aire cuando se le deja expuesto al Sol. A primera hora de la mañana, cuando aún no hace mucho calor, el globo tiene cierto volumen.
A medida que transcurre el tiempo y aumenta la temperatura, el globo también se calienta incrementando su volumen y todo ello ocurre a presión constante. El material del globo es un buen ejemplo de frontera lo bastante flexible como para que el aire en su interior, al calentarse, se expanda sin modificar la presión.
La experiencia también se puede llevar a cabo ajustando el globo sin inflar en el pico de una botella de vidrio llena con una tercera parte de agua, la cual se pone a calentar a baño de maría. Apenas el agua se calienta el globo se infla de inmediato, pero debe tenerse cuidado de no calentar demasiado para que no explote.
Es una nave flotante sin propulsión, que hace uso de las corrientes aéreas para transportar personas y objetos. El globo por lo general se llena con aire caliente, que al ser más frío que el aire circundante, se eleva y se expande haciendo que el globo ascienda.
Si bien las corrientes de aire dirigen al globo, este dispone de quemadores que se activan para calentar el gas cuando se desea ascender o mantener la altura, y se desactivan al descender o aterrizar. Todo esto sucede a presión atmosférica, supuesta constante a cierta altura no lejos de la superficie.

En las calderas se genera vapor calentando agua y manteniendo la presión constante. Después este vapor realiza un trabajo aprovechable, por ejemplo generar electricidad en centrales termoeléctricas o bien accionar otros mecanismos como locomotoras y bombas de agua.
Se tienen 40 litros de gas a 27 ºC de temperatura. Encontrar el incremento de volumen cuando se agrega calor isobáricamente hasta llegar a 100 ºC.
Solución
Se utiliza la ley de Charles para determinar el volumen final, pero atención: las temperaturas deben estar expresadas en kelvin, bastando con sumar 273 K a cada una:
27 ºC = 27 + 273 K = 300 K
100 ºC = 100 + 273 K = 373 K
A partir de:
V1/T1 = V2/T2 ⇒ V2 = T2(V1/T1)= 373 ºC (40 L/300 K) = 49.7 L
Finalmente el incremento de volumen es V2 – V1 = 49.7 L – 40 L = 9.7 L.
Se suministran 5.00 x 103 J de energía a un gas ideal para que realice 2.00 x 103 J de trabajo sobre su entorno en un proceso isobárico. Se pide hallar:
a) El cambio en la energía interna del gas.
b) El cambio en el volumen, si ahora la energía interna disminuye en 4.50 x 103 J y se expulsan 7.50 x 103 J del sistema, considerando presión constante de 1.01 x 105 Pa.
Solución a
Se utiliza ∆U = Q – W y se sustituyen los valores dados en el enunciado: Q = 5.00 x 103 J y W = 2.00 x 103 J:
=5.00 x 103 J – 2.00 x 103 J = 3.00 x 103 J
Por lo tanto la energía interna del gas aumenta en 3.00 x 103 J.
Solución b
El cambio de volumen se encuentra en el trabajo realizado: W = P∆V:
∆U = Q – W= Q – P∆V
El enunciado afirma que la energía interna disminuye, por lo tanto: ∆U= –4.50 x 103 J. También nos dice que se expulsa una cierta cantidad de calor: Q = -7.50 x 103 J. En ambos casos, el signo negativo representa disminución y pérdida, entonces:
–4.50 x 103 J = -7.50 x 103 J – P∆V
Donde P = 1.01 x 105 Pa. Como todas las unidades están en Sistema Internacional, se procede a despejar el cambio de volumen:
∆V = (-4.50 x 103 J +7.50 x 103 J)/ (- 1.01 x 105 Pa) = -2.97 x 10-2 m3
Como el cambio de volumen es negativo, significa que el volumen disminuyó, es decir, el sistema se contrajo.
- Byjou’s. Isobaric Process. Recuperado de: byjus.com.
- Cengel, Y. 2012. Termodinámica. 7ma Edición. McGraw Hill.
- Proceso xyz. Aprende más sobre el proceso isobárico. Recuperado de: 10proceso.xyz.
- Serway, R., Vulle, C. 2011. Fundamentos de Física. 9na Ed. Cengage Learning.
- Wikipedia. Leyes de los Gases. Recuperado de: es.wikipedia.org.
