Covarianza
La covarianza es el valor que refleja en qué cuantía dos variables aleatorias varían de forma conjunta respecto a sus medias.
Nos permite saber cómo se comporta una variable en función de lo que hace otra variable. Es decir, cuando X sube ¿Cómo se comporta Y? Así pues, la covarianza puede tomar los siguiente valores:
Covarianza (X,Y) es menor que cero cuando “X” sube e “Y” baja. Hay una relación negativa.
Covarianza (X,Y) es mayor que cero cuando “X” sube e “Y” sube. Hay una relación positiva.
Covarianza (X,Y) es igual que cero cuando no hay relación existente entre las variables “X” e “Y”.
Cálculo de la covarianza
La fórmula de la covarianza se expresa como sigue:
Dónde la y con el acento es la media de la variable Y, y la x con el acento es la media de la variable X. “i” es la posición de la observación y “n” el número total de observaciones.
Alternativamente, cuando las frecuencias absolutas no son unitarias (es decir, los pares i,j se repiten al menos una vez) la fórmula aplicable es la siguiente:
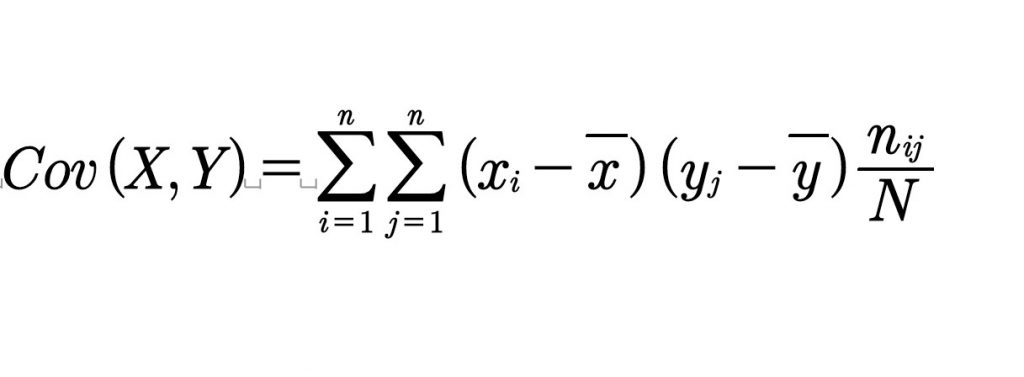
Propiedades de la covarianza
Han de tenerse en cuenta, a la hora de trabajar con ella las propiedades que tiene y que se deducen de la definición misma de covarianza:
- Cov (X, b) = 0, siendo b en este caso una constante.
- Cov (X, X) = Var(X) es decir, la covarianza de una variable y de sí misma es igual a la varianza de la variable.
- Cov (X, Y) = Cov(Y,X) la covarianza es la misma, independientemente del orden en que las pongamos.
- Cov (b·X, c·Y) = c·b ·Cov(X,Y) siendo b y c dos constantes. La covarianza de dos variables multiplicadas por dos constantes cualesquiera es igual a la covarianza de las dos variables multiplicada por la multiplicación de las constantes.
- Cov (b+X, c+Y) = Cov(X,Y) sumar dos constantes cualesquiera a cada variable, no afecta a la covarianza.
- Cov (X,Y) = E(X·Y) – E(X)·E(Y) o lo que es lo mismo, la covarianza es igual a la esperanza del producto de las dos variables menos el producto de las dos esperanzas por separado.
Ampliando las propiedades anteriores, en el caso de que dos variables sean independientes. Es decir, que no tengan relación estadística alguna, se cumple que:
E(X·Y) = E(X)·E(Y)
Es decir que la esperanza del producto de dos variables, es igual al producto de las dos esperanzas por separado de dichas variables.
Ejemplo de la covarianza
Supongamos que tenemos los siguientes datos de X e Y.
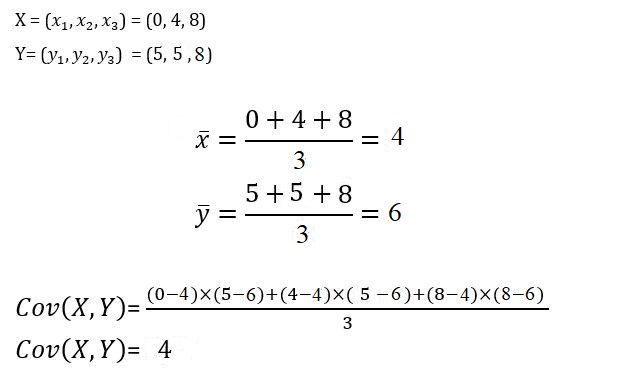
¿Cómo interpretamos este resultado?
Este 4 nos está diciendo, al ser mayor que cero, que estas dos variables tienen una relación positiva. Para saber la relación ajustada entre las dos variables deberíamos calcular la correlación lineal. Dos covarianzas de distintas variables no son comparables, ya que el valor de la covarianza es un valor absoluto que depende de la unidad de medida de las variables.
