Valor absoluto
El valor absoluto de un número real es la magnitud de este, independientemente del signo que le preceda.
El valor absoluto de un número, en otras palabras, es el valor que resulta de eliminar el signo correspondiente a este.
Para verlo en términos más formales, tenemos las siguientes condiciones que deben cumplirse, donde el x entre dos barras significa que estamos hallando el valor absoluto de x:
|x|=x si x≥ 0
|x|=-x si x<0
Es decir, el valor absoluto de un número positivo es este mismo número. En cambio, el valor absoluto de un número negativo es igual a este número, pero con un signo negativo delante. Es decir, multiplicado por -1.
Asimismo, el valor absoluto de -10 es -(-10)=10. Así, debemos destacar que el valor absoluto siempre es positivo.
Propiedades del valor absoluto
Entre las propiedades del valor absoluto destacan las siguientes:
- El valor absoluto de un número y de su opuesto es el mismo. Es decir, el valor de -19 y 19 es el mismo: 19.
- El valor absoluto de una sumatoria es igual, o menor, que la sumatoria de los valores absolutos de los sumandos. Es decir, se cumple que:
|x+y|≤|x|+|y|
Podemos comprobar lo anterior con algunos ejemplos:
|8+9|≤|8|+|9|
|17|≤8+9
17≤17
|12-25|≤|12|+|-25|
|-13|≤12+25
13≤37
|16+31-21|≤|16|+|31|+|-21|
|26|≤16+31+21
26≤68
- Otra propiedad es aquella a la que denominamos propiedad multiplicativa. Esta nos indica que el valor absoluto de un producto es igual al producto de los valores absolutos de los factores. Es decir, se cumple lo siguiente:
|xy|=|x|.|y|
Lo anterior podemos comprobarlo en los siguientes ejemplos:
|3×4|=|3|x|4|
|12|=3×4
12=12
|6x-5|=|6|x|-5|
|-30|=6×5
30=30
- Como contraparte de la propiedad multiplicativa, tenemos aquella de preservación de la división, la cual nos indica que el valor absoluto de una división es igual al cociente de los valores absolutos de los mismos elementos de dicha operación. Esto, siempre que el divisor no sea cero. Es decir, se cumple que:
|x/y|=|x|/|y|
Podemos verlo en algunos ejemplos:
|60/5|=|60|/|5|
|12|=60/5
12=12
|-87/3|=|-87|/|3|
|-29|=87/3
29=29
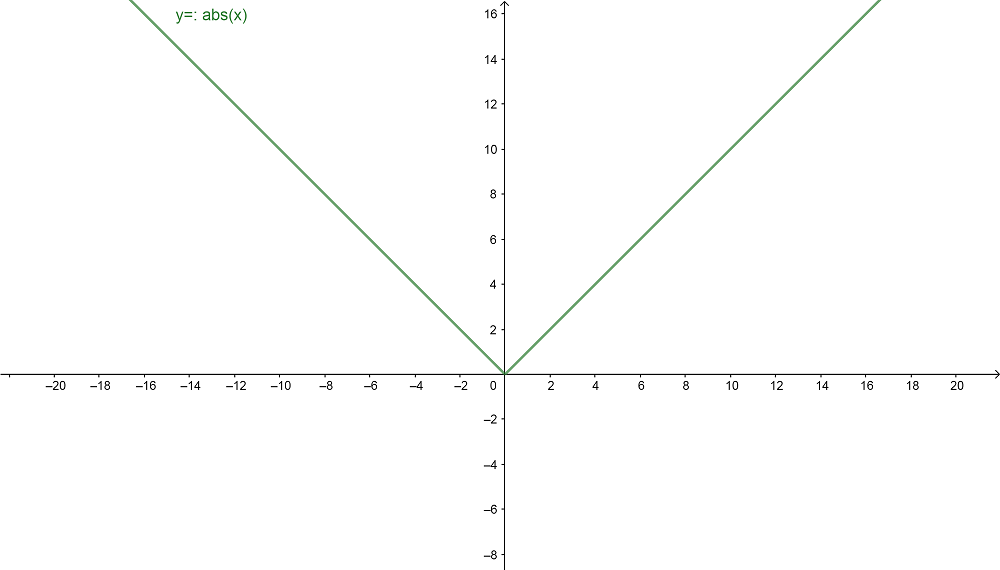
Valor absoluto en una gráfica
A continuación, veamos cómo quedaría un ejemplo del valor absoluto en un plano cartesiano.
En este caso, tenemos una simple función y=|x|, y observamos que el valor de y siempre será positivo, independientemente del valor de x.