Trapezoide
El trapezoide es un tipo de cuadrilátero que no tiene lados paralelos. Es decir, al ser prolongados, los segmentos que forman la figura podrían cruzarse.
A diferencia de otros cuadriláteros, el trapezoide no tiene lados paralelos. Además, pueden distinguirse de dos tipos, los simétricos (o deltoides) y los asimétricos.
El trapezoide simétrico es aquel donde dos de los lados continuos miden lo mismo, por lo que se dice que es simétrico respecto a su diagonal. Así, el cruce de las diagonales forma cuatro ángulos rectos (de 90º).
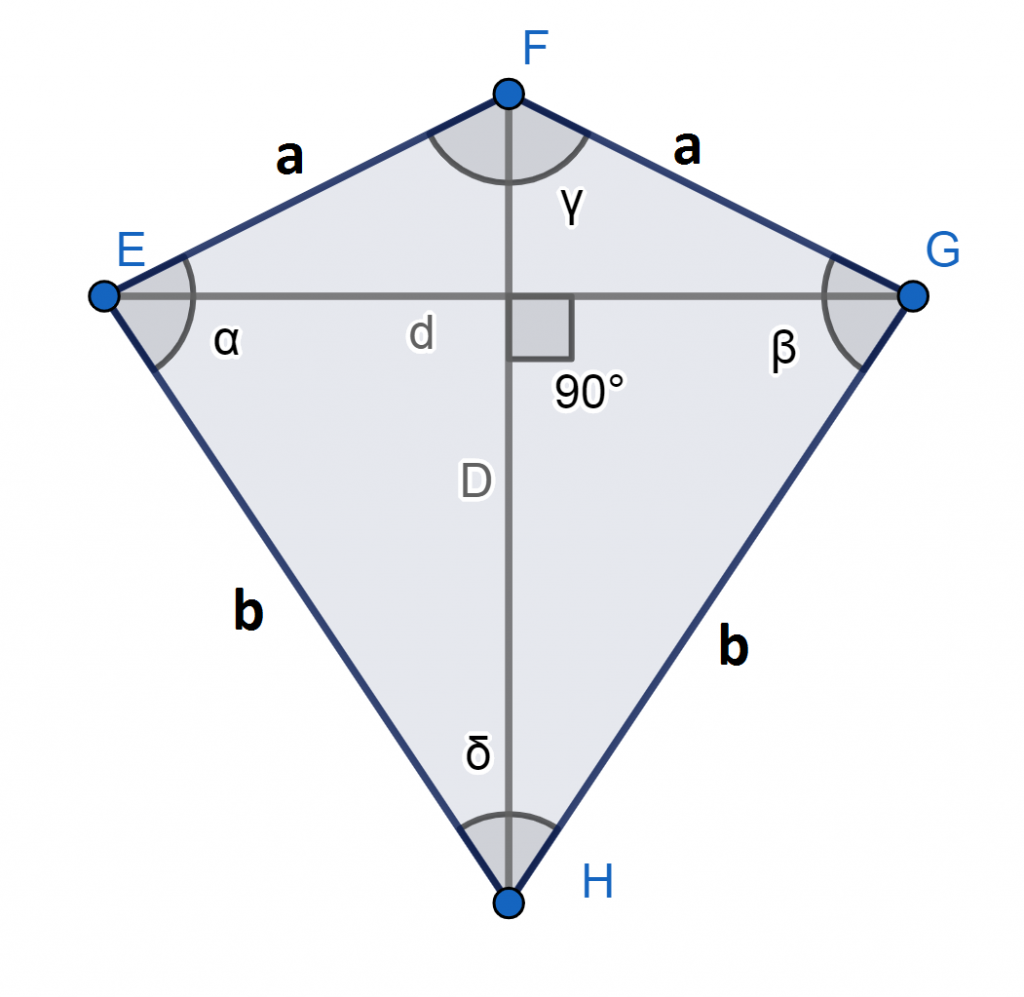
En la imagen inferior del trapezoide simétrico EF=FG y EH=GH
Elementos del trapezoide
Los elementos del trapezoide, como observamos en el siguiente gráfico, son los siguientes:
- Vértices: A, B, C, D.
- Lados: AB, BC, DC, AD.
- Diagonales: AC, DB.
- Ángulos interiores: α, β, δ, γ.
Perímetro y área de un trapezoide
Para conocer mejor las características de trapezoide, podemos calcular el perímetro y el área:
- Perímetro (P): Debemos sumar los cuatro lados del cuadrilátero.
- Área (A): Aquí podemos distinguir dos casos. Primero, cuando el trapezoide es asimétrico, podemos dividir la figura en dos triángulos (en la imagen inferior serían el triángulo ABC y el triángulo ADC), calcular el área de cada uno (como explicamos en el artículo de triángulo) y sumar ambos datos.
En el caso de un trapezoide simétrico seguiremos cualquiera de las siguientes fórmulas donde D y d son las longitudes de la diagonal mayor y menor respectivamente. Además, a y b son las longitudes de los lados (recordemos que tenemos dos pares de lados que miden lo mismo). Además, α es el ángulo que se forma entre dos lados de diferente longitud.
Ejemplo de trapezoide
Supongamos que tenemos un trapezoide simétrico donde sus lados miden 7 y 10 metros. Además, el ángulo que se forma entre dos lados que miden distinto es 45º. ¿Cuál es el perímetro y el área de la figura? (Tomemos en cuenta que al ser simétrico el trapezoide tiene dos pares de lados de igual longitud).
P = 7 + 7 + 10 + 10 = 24 m
Asimismo, para calcular al área utilizamos la segunda fórmula propuesta:
A = 7 x 10 x sen(45º)= 49,4975 m2
Otros trapezoides
En el artículo, solo hemos mencionado el caso de los trapezoides convexos, pero debemos mencionar que existen trapezoides cóncavos, cuando alguna de las diagonales es externa, como vemos en la siguiente imagen:
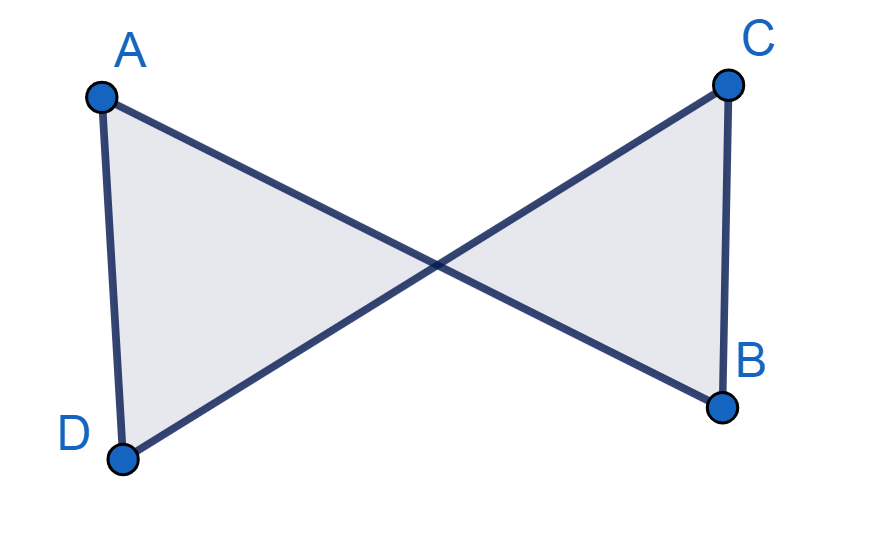
Asimismo, tenemos aquel caso del trapezoide cruzado cuando dos de sus lados se intersecan, formando dos triángulos, como observamos en el siguiente gráfico: