Cuadrilátero

Cabe señalar que un polígono es una figura bidimensional cerrada constituida por un número finito de segmentos consecutivos. A los segmentos se les denomina lados y a sus intersecciones, vértices.

El cuadrilátero es entonces una figura de cuatro lados, los cuales pueden o no ser de igual longitud. Asimismo, tiene cuatro ángulos interiores y exteriores, que corresponden a cada vértice.

Además, cada cuadrilátero cuenta con dos diagonales, que son aquellos segmentos que unen un lado o vértice de una figura geométrica con el lado opuesto.

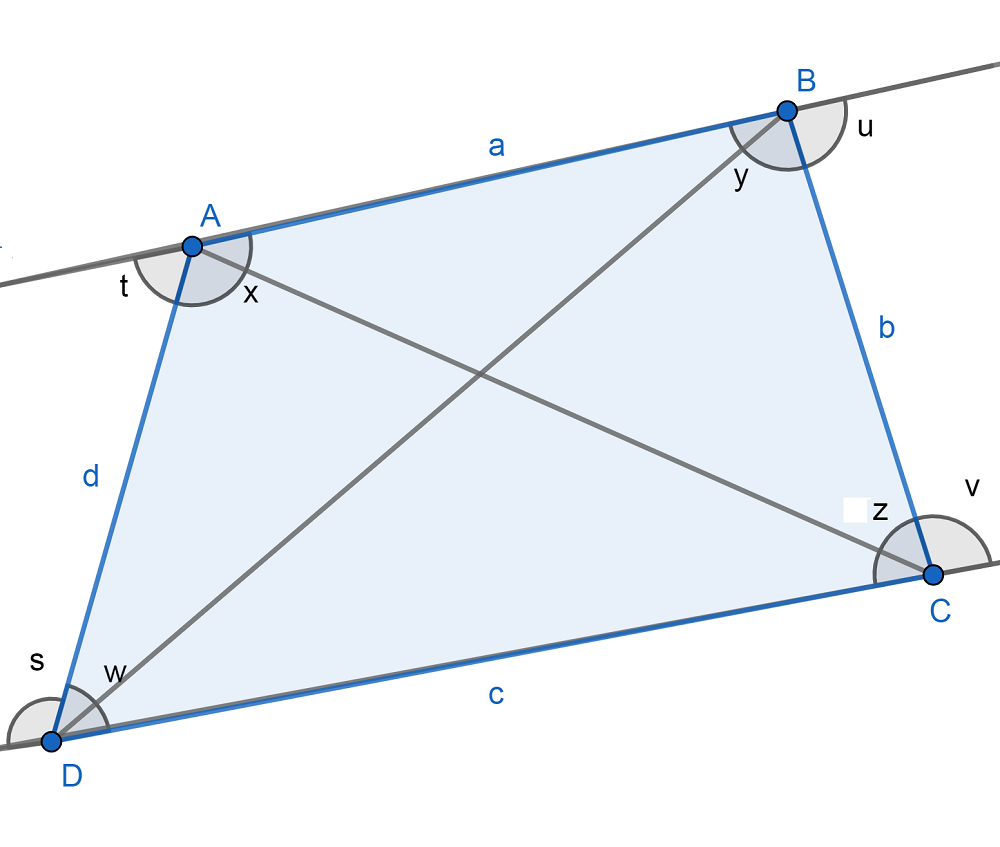
Guiándonos del gráfico en la parte inferior, los elementos de cuadrilátero son los siguientes:

• Vértices: A,B,C,D.
• Lados: AB,BC,DC,AD.
• Ángulos interiores: w,x,y,z. Suman 360º.
• Ángulos exteriores: s,t,u,v.
• Diagonales: Son los segmentos de recta que unen vértices opuestos de la figura. Son AC y DB.

Los tipos de cuadrilátero son:

• Paralelogramo: Es un cuadrilátero donde los lados opuestos son paralelos entre sí (los segmentos no llegarían a intersecarse aunque fueran prolongados) y miden la misma longitud. Es una categoría dentro de la cual se encuentran otras varias.
  • Cuadrado: Es un tipo de paralelogramo con cuatro lados de igual longitud y paralelos entre sí. Sus ángulos interiores son rectos, es decir, miden 90º. Sus diagonales son perpendiculares entre sí (cuando se cortan forman cuatro ángulos de 90º).
  • Rectángulo: De sus cuatro lados, hay dos pares de lados de igual longitud. Todos sus ángulos interiores miden 90º. Sus diagonales miden lo mismo, pero no son perpendiculares entre sí.
  • Rombo: Todos sus lados tienen la misma longitud. Dos de sus ángulos interiores son agudos (menores a 90º), miden igual y están uno frente al otro. En tanto, los otros dos ángulos interiores son obtusos (mayores a 90º) y también miden lo mismo. Sus diagonales son perpendiculares entre sí, pero miden diferente.
  • Romboide: Tiene dos pares de lados que se corresponden en longitud y tiene dos ángulos interiores agudos y dos obtusos. Cada par de ángulos, que miden también lo mismo, están uno frente al otro.

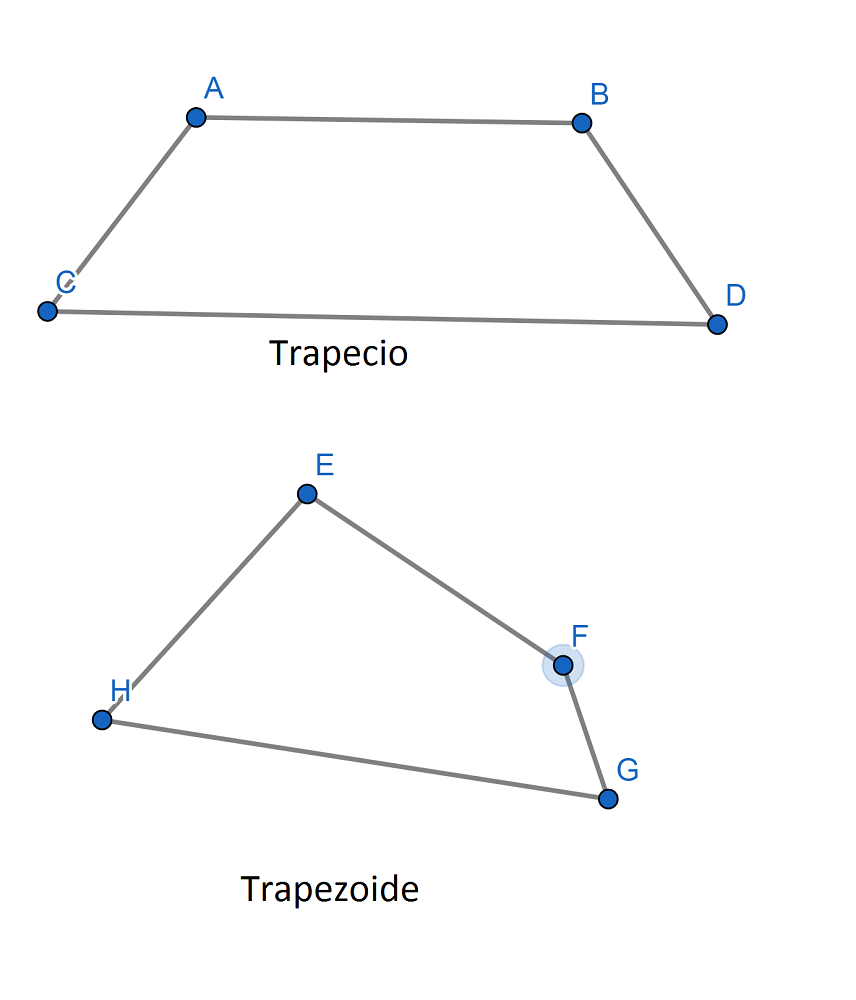
• Trapecio: Tiene solo dos lados que son paralelos entre sí, llamados base del trapecio, y que tienen diferente longitud. La altura del trapecio es el segmento de recta que une ambas bases o sus prolongaciones.
• Trapezoide: Es un cuadrilátero sin lados paralelos.

También se puede clasificar a los cuadriláteros en función de la medida de sus ángulos:

• Cóncavos: Cuando al menos uno de sus ángulos interiores es mayor a 180°.
• Convexos: Cuando ninguno de sus ángulos interiores mide más de 180°. 

Para conocer mejor las características de un cuadrilátero podemos calcular lo siguiente:

• Perímetro(P): Es la suma de los lados:

P=AB+BC+CD+AD

• Área(A): La complejidad cálculo varía en cada caso. En un cuadrado, por ejemplo, solo se eleva la longitud del lado al cuadrado. Sin embargo, se pude aplicar una fórmula que aplica a todo tipo de cuadrilátero:

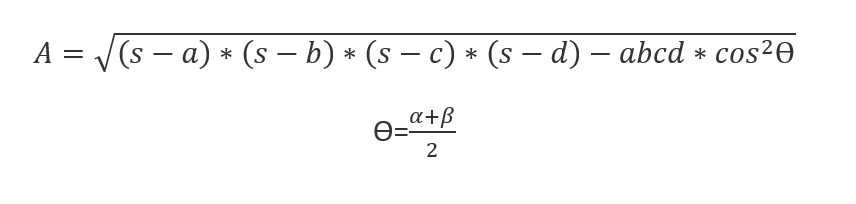
Donde s es el semiperímetro (P/2), y α y β son dos ángulos opuestos del cuadrilátero. Asimismo, a,b,c y d son las longitudes de los lados, y cos indica que se calculará el coseno de un ángulo.

Supongamos que tenemos un cuadrilátero cuyos lados y sus longitudes respectivas son las siguientes (todo medido en metros):

AB: 23

BC: 10

AC: 25

AD: 12

Asimismo, el ángulo formado entre AB Y BC es 40º y el que forman CD y AD es 60º ¿Cuál es el perímetro y el área del cuadrilátero?

P= 23+10+25+12= 70 metros

Entonces, para calcular el área primero hallamos el semiperímetro y aplicamos la fórmula mostrada en el apartado anterior: