Regla de Laplace
La regla de Laplace es un método que permite calcular rápidamente el determinante de una matriz cuadrada con dimensión de 3×3 o mayor mediante una serie de expansión recursiva.
En otras palabras, la regla de Laplace factoriza la matriz inicial en matrices de menor dimensión y ajusta su signo en función de la posición del elemento en la matriz.
Este método se puede desarrollar mediante filas o columnas.
Artículos recomendados: matrices, tipologías de matrices y determinante de una matriz.
Fórmula la regla de Laplace
Dada una matriz Zmxn cualquiera de dimensión mxn,donde m=n, se expande respecto a la i-ésima fila, entonces:
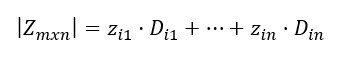
- Dijes el determinante obtenido de eliminar la i-esima fila y la i-esima columna de Zmxn.
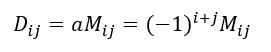
- Mijes el i,j-esimo menor. El determinante Dijen función de Mijse denomina el i,j-esimo cofactorde la matriz Zmxn.
- a es el ajuste de signo de la posición.
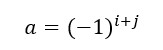
Ejemplo teórico regla de Laplace
Definimos A3×3 como:
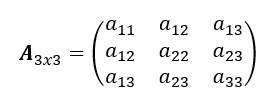
- Empecemos por el primer elemento a11. Rallamos las filas y columnas que integren a11. Los elementos que queden sin rallar, será el primer determinante menor multiplicado por a11.
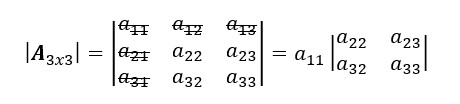
2. Seguimos con el segundo elemento de la primera fila, es decir, a12. Repetimos el proceso: rallamos las filas y columnas que contengan a12.
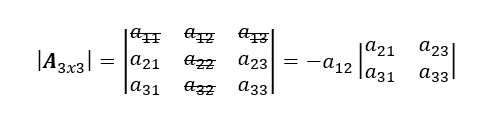
Ajustamos el signo del menor:
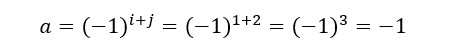
Añadimos el segundo determinante menoral resultado anterior y formamos una serie de expansión tal que:
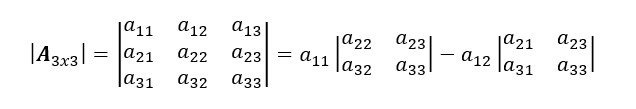
3. Continuamos con el tercer elemento de la primera fila, es decir, a13. Repetimos el proceso: rallamos la fila y la columna que contengan a13.
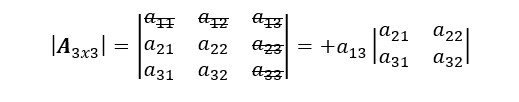
Añadimos el tercer determinante menor al resultado anterior y ampliamos la serie de expansión tal que:
Dado que ya no quedan más elementos en la primera fila, entonces cerrramos el proceso recursivo. Calculamos los determinantes menores.
De la misma forma que se han empleado elementos de la primera fila, este método también se puede aplicar con las columnas.
Ejemplo práctico regla de Laplace
Definimos A3×3como:
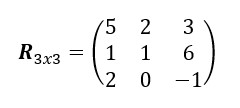
1. Empecemos por el primer elemento r11=5. Rallamos las filas y columnas que integren a11=5. Los elementos que queden sin rallar, será el primer determinante menor multiplicado por a11=5.
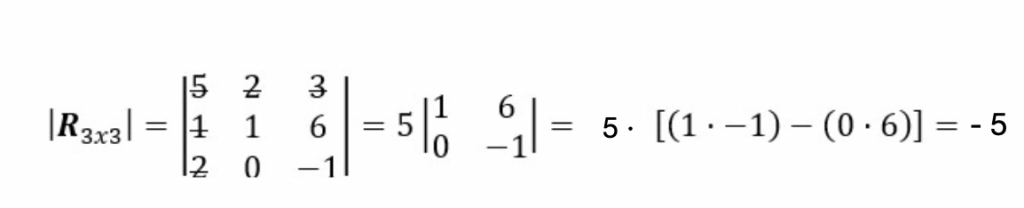
2. Seguimos con el segundo elemento de la primera fila, es decir, r12=2. Repetimos el proceso: rallamos las filas y columnas que contengan r12=2.
Ajustamos el signo del menor:
Añadimos el segundo determinante menor al resultado anterior y formamos una serie de expansión tal que:
3. Continuamos con el tercer elemento de la primera fila, es decir, r13=3. Repetimos el proceso: rallamos la fila y la columna que contengan r13=3.
Añadimos el tercer determinante menor al resultado anterior y ampliamos la serie de expansión tal que:
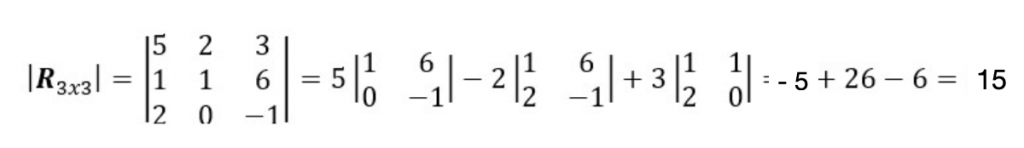
El determinante de la matriz R3×3 es 15.
