Normalización estadística

En otras palabras, la normalización son proporciones sin unidades de medida (adimensionales o invariantes de escala) que nos permiten poder comparar elementos de distintas variables y distintas unidades de medida.

En estadística y econometría se emplean tablas de distribución de probabilidad tipificadas para encontrar la probabilidad que tome una observación dada la función distribución que siga la variable. 

Es importante no limitar el término de normalización solo a conjuntos de elementos donde la distribución normal sea una buena aproximación a su frecuencia.

En la siguiente tabla se detallan las normalizaciones más comunes en estadística aplicada a las finanzas y economía.

• La puntuación tipificada o estándar normaliza los errores cuando podemos calcular los parámetros muestrales.
• La normalización en la distribución T de Student normaliza los residuos cuando los parámetros son desconocidos y hacemos una estimación para obtenerlos.
• El coeficiente de variación utiliza la media como medida de escala a diferencia de la puntuación tipificada y la T de Student que utilizan la desviación estándar. La distribución se normaliza para las distribuciones de Poisson y exponencial.
• El momento estandarizado puede aplicarse a cualquier distribución de probabilidad que tenga una función generadora de momentos. En otras palabras, que las integrales de los momentos sean convergentes.

¿Cuantas veces hemos leído que la distribución de probabilidad normal parece una suficiente buena aproximación a la frecuencia de las observaciones y nos piden encontrar la probabilidad de que la variable X tome un valor concreto?

En otras palabras, establecemos X~N(μ,σ²), y nos piden encontrar P(X ≤ x_i)

Sabemos que para encontrar P(X ≤ x_i) , necesitamos buscar la probabilidad en las tablas de distribución de probabilidad. En este caso, en las tablas de la distribución de la distribución normal. Las tablas de distribución de probabilidad más usadas en econometría y finanzas cuantitativas son: ji-cuadrado, t de Student, F de Fisher-Snedecor, Poisson, exponencial, cauchy y la normal estándar.

Las probabilidades calculadas en las tablas de distribución cumplen la propiedad:

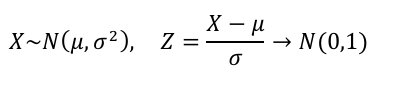
Es decir, las probabilidades (los números dentro de la tabla) están tipificadas. Entonces, tendremos que tipificar también nuestra variable según los parámetros de la función de distribución si queremos encontrar la probabilidad de P(X ≤ x_i).

Queremos saber la probabilidad de que el número de esquiadores que vayan a esquiar un viernes por la mañana sea de 288.

La estación de esquí nos dice que la frecuencia de la variable esquiadores puede aproximarse a una distribución normal de media 280 y varianza 16.  

Entonces, tenemos:

X~N(μ,σ²)

donde X la definimos como la variable ‘esquiadores’

Nos piden, la probabilidad de que el número de esquiadores que van a esquiar un viernes sea menor o igual que 288. Es decir:

P(X ≤ 288)

Para buscar la probabilidad de que el número de esquiadores sea igual a 288, primero tenemos que tipificar la variable.

Luego miramos la tabla de distribución de la normal estándar continua:

Z	0	1	2	3
2,0	0,9772	0,9778	0,9783	0,9788

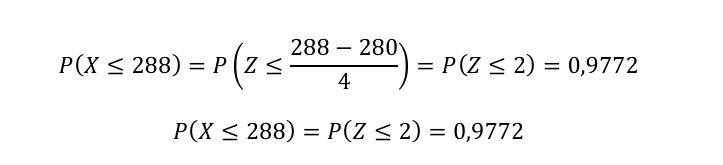
La probabilidad de que un viernes por la mañana 288 esquiadores vaya a esquiar es de 97,72% dados los parámetros media y varianza.