Módulo de un vector y el teorema de Pitágoras
El módulo de un vector es la longitud de un segmento orientado en un espacio que está determinado por dos puntos y el orden de estos.
En otras palabras, el módulo de un vector es la longitud entre el inicio y el final del vector, es decir, dónde empieza y dónde termina la flecha.
Dado un vector cualquiera de dos dimensiones:
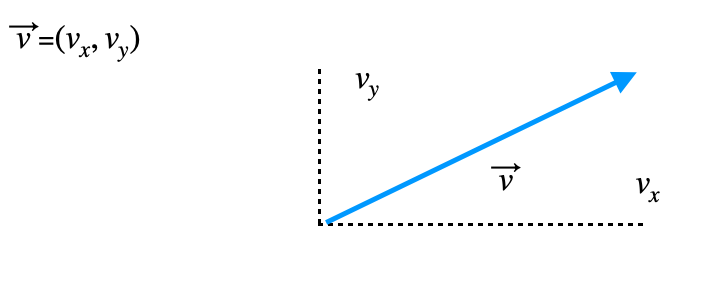
La información que nos dan las coordenadas del vector, es decir vx y vy, es su longitud para el eje x y su longitud para el eje y, respectivamente.
Entonces, si conocemos las coordenadas podemos calcular el módulo del vector.
Módulo de un vector y el teorema de pitágoras
¿El dibujo anterior no os recuerda a una figura geométrica?
Exacto, podemos imaginar que los ejes de coordenadas al lado del vector forman un rectángulo de base vx y de altura vy. Este rectángulo lo podemos dividir en dos triángulos simétricos, es decir, que ambos tendrán la misma base y altura.
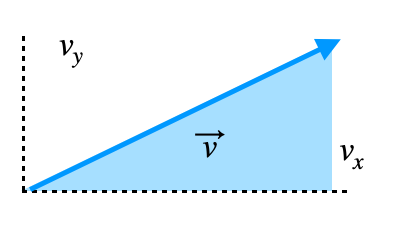
El triángulo sombreado de azul tiene una base de vx y una altura de vy. Entonces, conociendo esta información podemos saber su hipotenusa. Existe un teorema muy famoso conocido como teorema de Pitágoras que se emplea para estos cálculos.
Demostración
Sabemos que la fórmula de Pitágoras es la siguiente:
Donde h es la hipotenusa, c es un cateto y c es otro cateto.
En nuestro caso, sabemos cuánto valen nuestros catetos, en otras palabras, la base y la altura. Entonces, podemos sustituir esa información en la ecuación:
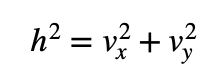
Procedemos a quitar el cuadrado de la h aplicando la raíz cuadrada:
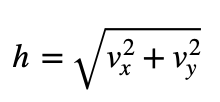
Si decimos que vx = 3 y vy = 6:
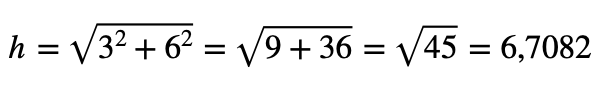
Por tanto, si v fuera un vector con coordenadas (3,6), entonces sabríamos que su módulo es de 6,7082. Exacto, su módulo, porque la fórmula del módulo de un vector v cualquiera es:
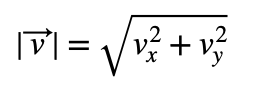
Vemos que precisamente la información que nos falta en la ecuación coincide con la hipotenusa. En otras palabras, la longitud del vector es lo queremos calcular y la hipotenusa es la diagonal del triángulo. Por tanto, podemos concluir que emplear el teorema de Pitágoras para calcular el módulo del vector es un método válido.
Entonces, si necesitamos calcular el módulo de un vector y no nos acordamos de la fórmula, podemos pensar en el teorema de Pitágoras y solucionar el problema.
Ejercicio resuelto
Calcula el módulo del vector v con coordenadas (-3,-6) aplicando el teorema de Pitágoras.
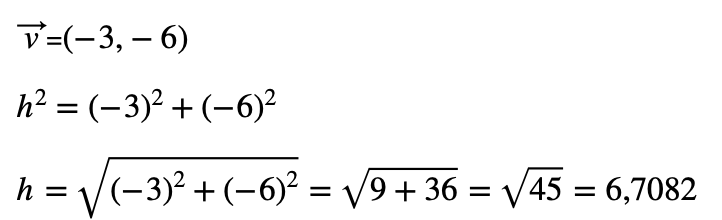
El módulo del vector v con coordenadas (-3,6) calculado a partir de la fórmula del teorema de Pitágoras es también de 6,7082.
