Modelo de Vasicek

En otras palabras, el modelo Vasicek se utiliza para predecir los tipos de interés a largo plazo mediante la simulación de tipos de interés a corto plazo. Además, tiene en cuenta que los tipos de interés son distintos en diferentes períodos de tiempo (estructura temporal de los tipos de interés). 

Los modelos de equilibrio sobre tipos de interés utilizan los tipos de interés de más corto plazo para calcular los tipos de interés futuros teniendo en cuenta la estructura temporal de los tipos de interés.

Para construir la curva de tipos necesitamos los tipos de interés a corto plazo y los parámetros del modelo. Una vez tenemos los tipos de interés a corto plazo y los parámetros podemos calcular los tipos de interés a largo plazo. 

Entonces, para calcular los precios de los bonos cupón cero a futuro, necesitamos los tipos de interés cupón cero a corto plazo. De esta forma, también podremos construir la curva o estructura temporal de tipos de interés cupón cero. Una vez tenemos la curva, determinaremos la evolución de los tipos de interés a largo plazo dados los tipos de interés de corto plazo. 

Solución analítica para encontrar el precio de un bono cupón cero que paga 1€ a vencimiento (T) en un período de tiempo (t) cualquiera y a un tipo de interés a corto plazo (r(t)).

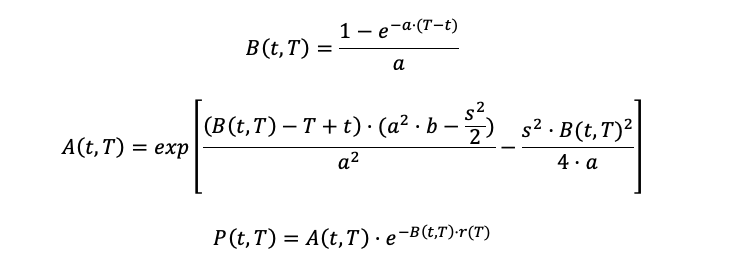
¡Qué no cunda el pánico! 

Solo necesitamos:

• El período de tiempo en el cual queremos saber los tipos de interés, es decir, T.
• El momento de tiempo en el cual nos encontramos ahora o el momento de inicio que queramos, es decir, t.
• La curva de interés a corto plazo, es decir, r(T) o r_T . Si quisiéramos expresar los tipos de interés en el período de inicio, utilizaríamos r(T) o r_T.
• En estas fórmulas trataremos los parámetros a, b y s como constantes en el tiempo.
• La desviación estándar, s.

Para calcular el precio de un bono cupón cero que paga 1€ a vencimiento (T) en un período de tiempo (t) cualquiera solo tenemos que dar valores a los parámetros a, b y s y simular los tipos de interés a corto plazo (r(t)). 

P(t,T) representa el precio del bono desde el instante t hasta T.

En absoluto, como hemos dicho al principio, los tipos de interés dependen de un proceso geométrico Browniano, y por tanto, implica la presencia de un componente aleatorio, N(0,1). Entonces, cada vez que calculemos las fórmulas anteriores, los tipos a corto plazo cambiarán y así también lo harán los tipos de interés a largo plazo, los precios de los bonos y su representación.

Utilizaremos las siguientes fórmulas para encontrar r(T) y R(T).

Fórmula tipos de interés a corto plazo (r_T): 

Fórmula tipos de interés a largo plazo (R_T):