Método Vogel

El método Vogel, por tanto, tiene como objetivo principal minimizar dichos costes. Cuando decimos que es heurístico, nos referimos a que utiliza criterios sencillos para la solución de problemas difíciles. Además, tiene una ventaja sobre otros porque, aunque precisa de más iteraciones, sus resultados iniciales –no ficticios– son mejores. Es similar a otros métodos, como el método húngaro.

Con la llegada de la Revolución Industrial, los problemas empresariales crecieron. Entre ellos, los de asignación de tareas y costos. Por esta razón, surgieron algunos métodos que permitían hacerlo de forma eficiente. Así, en 1955, Harold W. Kuhn plantea el método húngaro, a la vez que comienzan a desarrollarse otros similares en la rama de administración de operaciones.

Uno de los problemas principales surge en el transporte. El objetivo es cómo decidir rutas, tiempos o destinos, basándonos en la necesidad de minimizar los costos y poder satisfacer la demanda con la oferta disponible. William R. Vogel propone, para ello, el método que recibe su nombre. Un método que, por medio de un algoritmo, resuelve los problemas relacionados con los transportes y su asignación.

La principal ventaja del método Vogel es que utiliza una serie de penalizaciones para calcular el coste mínimo, así como que su cálculo es sencillo. Por otro lado, el principal inconveniente es que requiere de mayores esfuerzos que otros y, en base a esto, no aporta un criterio para decidir si la solución es la mejor.

Pero, dicho esto, repasemos los pasos que debemos dar para realizarlo; aunque lo veremos con más detalle en el ejemplo:

• En primer lugar, debemos calcular una penalización que añadiremos a la matriz inicial. Para realizar este paso se restan los dos costos menores en cada fila y columna. A continuación, se utiliza aquella fila o columna con una mayor penalización. Si hubiera dos valores máximos iguales, la elección es a juicio de quien realiza el análisis.
• A continuación, debemos fijarnos en aquella fila o columna que habíamos elegido. Escogemos la celda que tenga un costo menor y le asignamos el mayor número de unidades de demanda que podamos, teniendo en cuenta la oferta disponible. De esta forma, el resto de esa fila o columna será cero y la podremos eliminar.
• Por último, hay que tener en cuenta una serie de reglas finales. Si queda solo una fila se detiene el algoritmo. Si esta tiene valores positivos, hay que determinar las variables básicas de la solución. En caso contrario, se vuelve al punto primero y se reinicia el proceso.

Con el fin de comprender mejor dicho concepto, a continuación, se expone un ejemplo de este.

Imaginemos que tenemos una serie de plantas productivas, que deben suministrar bienes a ciertos destinos. En primer lugar, creamos la tabla inicial de doble entrada que muestra los costes unitarios de cada opción. Por otro lado, las capacidades de oferta (O) y las necesidades de demanda (D) se muestran en la fila y columna correspondiente, así como en la tabla de la derecha (Figura 1).

En el primer paso, se calculan las penalizaciones (Pe1), como se explicó antes, y se elige la mayor de ellas, el tres (azul oscuro) de la casilla (Pe1, D3). Escogemos el menor valor de esa columna, que sería el cuatro (azul intermedio) de la casilla (P2, D3). En la tabla de la derecha, en la misma posición, se inserta el mayor valor posible según la demanda de esa columna, que es 30 (gris). Por tanto, sobrarían 10 en la oferta, ya que su máximo son 40.

Así pues, volvemos a realizar el proceso en el paso 2, una vez eliminada la columna D3. Calculamos la segunda penalización (Pe2), y repetimos los pasos anteriores. La fila elegida será la P1, con el menor valor de cinco y con un valor máximo en la tabla de oferta y demanda de cincuenta. En el paso 3, hacemos lo mismo, incluyendo la tercera penalización (Pe3).

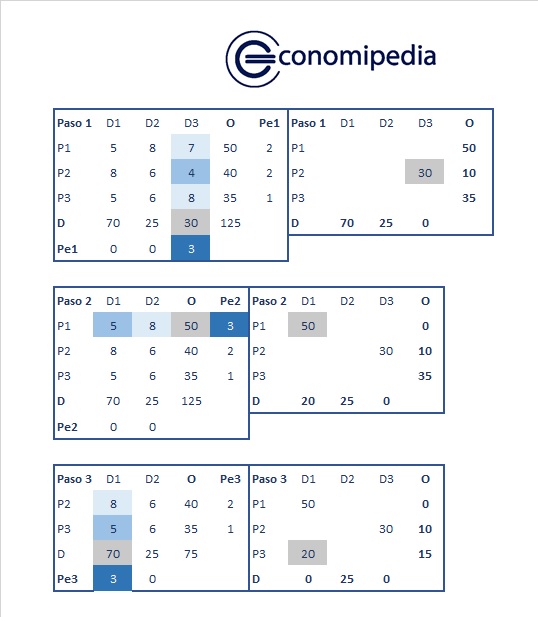
Como vemos, en la figura 2 solo aparece la columna D2 y todos los valores son positivos. En este sentido, hemos llegado al final. Ahora, tomando esas dos posiciones (P2D2;P3D2) en la tabla de oferta y demanda, vemos qué valores faltarían para que todo sea cero. En este caso, los números que faltan son el diez y el quince.

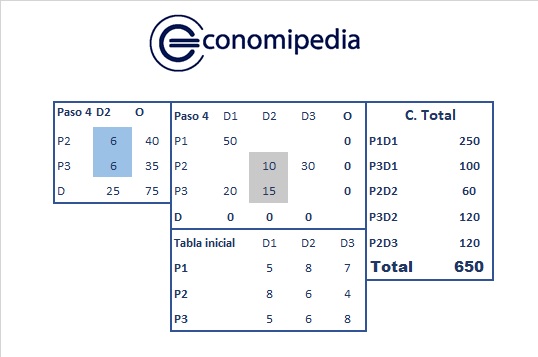
Por último, podemos ver que el método Vogel ofrece un coste total, que se calcula multiplicando esos datos de la derecha por sus costes unitarios de la izquierda. Hemos insertado la tabla original del principio para facilitar el cálculo. El coste total será de 650 y, a su vez, podemos observar los parciales de cada opción.