Mayor que

La expresión «mayor que» es utilizada en matemáticas, concretamente en una desigualdad matemática. Esta desigualdad matemática puede ser entre números, incógnitas y funciones de diferentes tipos.

Por ejemplo, para decir que 5 es mayor que 3, podemos expresarlo así:

5 > 3

O, también podríamos ponerlo así.

3 < 5

En general, tenemos tres símbolos para comparar expresiones matemáticas:

• Igual ( = )
• Mayor que
• Menor que

Los símbolos para «mayor que» y «menor que» son los mismos. Lo único que, dependiendo dónde se sitúe la parte abierta y la parte cerrada, deberemos poner el símbolo en una dirección u otra.

Existe un truco para no confundirnos nunca con los signos → la parte abierta señala siempre al número más grande.

Comparar dos números es muy sencillo. Por ejemplo, sabemos que 10 es mayor que 2, que 3 es mayor que 2 o que 21 es mayor que 20. Sin embargo, cuando entran en juego funciones matemáticas la cosa cambia un poco. Veamos un ejemplo

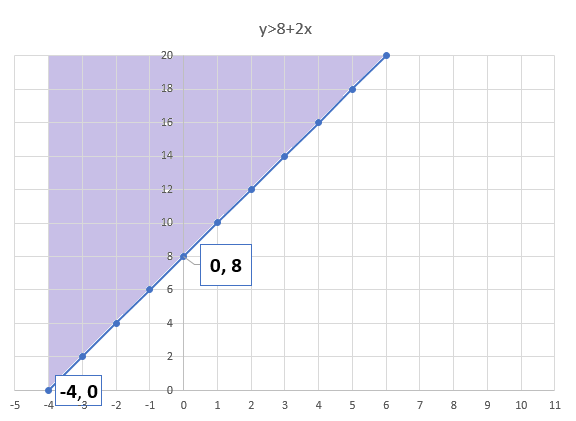
Supongamos que queremos graficar que y>8+2x

Entonces, primero tomamos la ecuación como una igualdad y despejamos aquellos puntos donde las variables son iguales a cero

si y=0

0=8+2x

x=-4

Por ende, el punto en el plano cartesiano sería (-4,0)

si x=0

y=8

Por tanto, el punto en el plano cartesiano sería (8,0)

Podemos observar entonces en el gráfico que el área sombreada es lo que correspondería a la ecuación y>8+2x

Ahora, supongamos que tengo la siguiente ecuación de segundo grado:

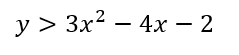
Entonces, primero tomamos la ecuación de la derecha y dibujamos la parábola que corresponde cuando la igualamos a cero.

Cuando resolvemos la ecuación, encontramos que los valores de x cuando y es igual cero son – 0,3874 y 1,7208. Entonces, esos son los dos puntos por donde debe pasar la parábola como vemos en el siguiente gráfico (La ecuación la pueden resolver en una calculadora en línea).

En el gráfico, la parábola cruza el eje x cuando el valor de x es -0,3874 (lo aproximamos a -0,39) y 1,7208 (o 1,72).

Luego despejamos el valor de y cuando x es igual a cero, que es -2 (el punto negro en el gráfico). Finalmente, para encontrar cuál debe ser el área a sombrear cambiamos x e y por 0:

0>0-0-2

0>-2

Como esto se cumple, debemos sombrear el área donde se encuentra el punto (0,0), es decir, dentro de la parábola, que es lo que correspondería a la desigualdad.