Logaritmo
El logaritmo es una función monótona estrictamente cóncava (creciente) comprendida en el conjunto de los números reales positivos y es la inversa de la función exponencial.
En otras palabras, el logaritmo es una función que depende de una base y un argumento que crece a una tasa de crecimiento cada vez menor.
Artículos recomendados: logaritmo natural, logaritmos en econometría y números reales.
Fórmula del logaritmo
La expresión del logaritmo está compuesta por una base y un argumento.
En este caso, la base es x y el argumento es z a partir de los cuales obtendremos el logaritmo.
Pero… De los elementos de la ecuación anterior, ¿cuál es el logaritmo?
Mayoritariamente tendemos a pensar que el logaritmo de la expresión anterior es solo logx, pero no es cierto. La respuesta correcta es logxz dado que también necesitamos la variable z para poder calcular el logaritmo.
Dominio
Dada una variable numérica z comprendida dentro del conjunto de los números reales, está sujeta a la restricción de adoptar solo los reales positivos.
En otras palabras, los argumentos de los logaritmos solo tomarán números reales estrictamente (>) mayores a cero (0).
Dado un número x comprendido dentro del conjunto de los números reales, está sujeto a la restricción de adoptar solo los reales positivos mayores a 1.
En otras palabras, las bases de los logaritmos solo tomarán números reales estrictamente (>) mayores a uno (1).
Las bases más utilizadas son 2, 10 y e.
El logaritmo en base 10 se denomina logaritmo decimal o común.
El logaritmo en base 2 se conoce como logaritmo binario.
Si la base del logaritmo es el número e, entonces el logaritmo se denomina logaritmo natural o neperiano.
Representación
¿Qué necesitamos para calcular el logaritmo de un número?
Para calcular el logaritmo necesitamos dos números que pertenezcan al conjunto de los reales positivos y además que uno de ellos sea distinto de uno (1). Un número actuará como argumento y el otro como base, respectivamente.
Resultado
Aunque haya restricciones en los números que puedan utilizarse para la base y el argumento, el codominio de la función logarítmica son todos los números reales. En otras palabras, podemos obtener logaritmos negativos, neutrales (0) o positivos dado que pueden tomar cualquier valor de la recta real:
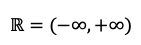
Es importante no confundir el dominio del argumento con el dominio del resultado (codominio).
Ejemplos
Aplicación
En finanzas se utilizan los logaritmos para obtener las rentabilidades continuas de un activo o producto financiero.
En economía, tanto en microeconomía como en macroeconomía, se utilizan para expresar la aversión al riesgo de los agentes económicos en las funciones de utilidad. También se utilizan para hacer transformaciones monótonas de las funciones de utilidad.
En econometría se transforma la escala de las variables para facilitar su interpretación.
