Geometría analítica

La geometría analítica localiza, en un plano bidimensional, cada uno de los puntos que forman una figura. Todo ello, en función de dos rectas, el eje de abscisas (eje horizontal X) y de las ordenadas (eje vertical Y).

Los ejes X e Y son perpendiculares. Es decir, forman cuatro ángulos de 90º (grados) en su intersección. De ese modo, se trabaja en un sistema de coordenadas que se conoce como plano cartesiano.

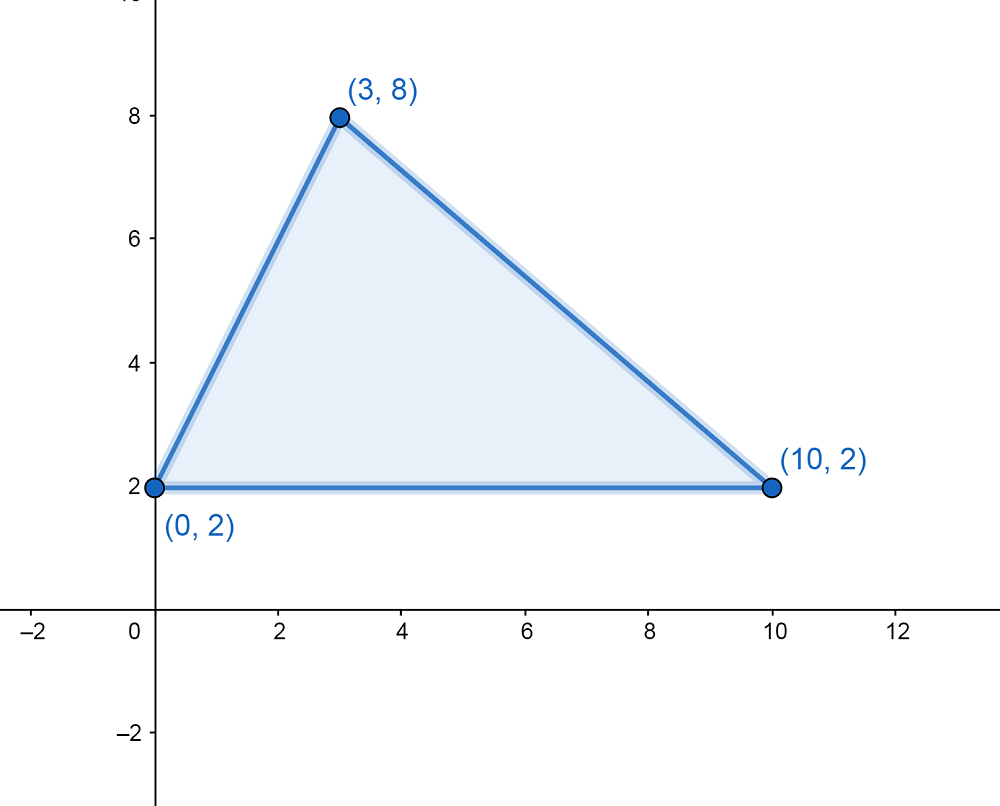
Cada punto del plano posee una coordenada del siguiente tipo (X,Y). Así, el punto (3,8) es aquel que nace de unir el punto 3 en el eje horizontal y el punto 8 en el eje vertical.

Un dato importante a mencionar es que se considera al filósofo René Descartes como el padre de la geometría. Especialmente, tras la publicación de su obra El Discurso del Método, y particularmente, en uno de sus apéndices llamado La Géométrie.

Para simplificar, lo que propone la geometría analítica es unir el álgebra con la geometría o, para ser más precisos, aplicar la primera disciplina en la segunda, como quedará más claro a continuación.

Al aplicar la geometría analítica podemos describir una figura geométrica mediante una ecuación algebraica.

En el caso de una recta, por ejemplo, podemos definirla como una ecuación de primer grado como la siguiente:

y = xm+b

En la ecuación mostrada, Y es la coordenada en el eje de las ordenadas (vertical), X es la coordenada en el eje de las abscisas (horizontal), m es la pendiente( inclinación) que forma la recta respecto al eje de las abscisas, y b es el punto de la recta que corta el eje de las ordenadas.

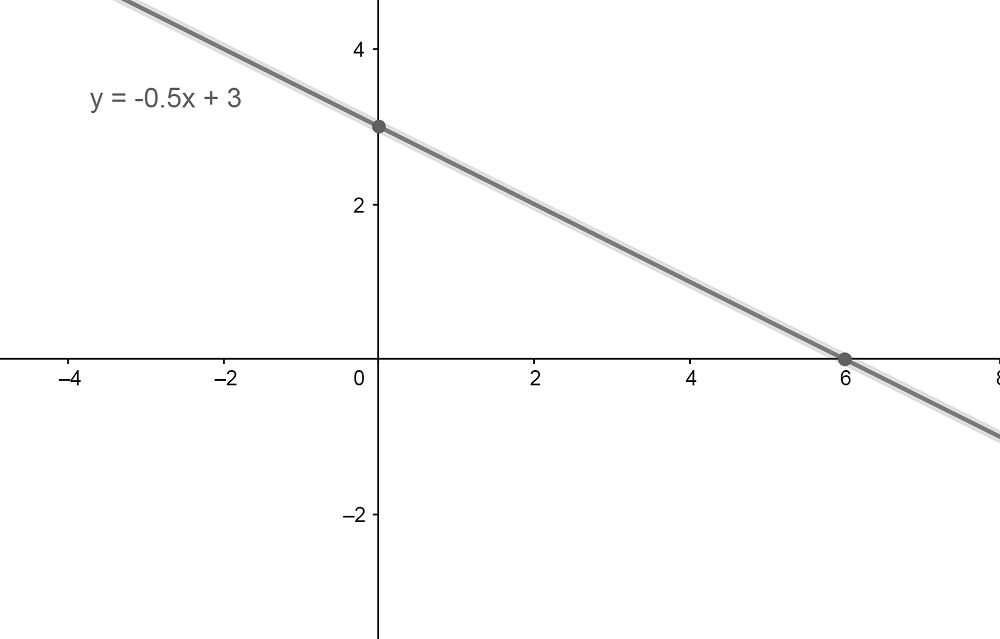
Por ejemplo, podemos graficar la recta con la ecuación: y=-0,5x+3

Sabiendo las ecuaciones de dos rectas, podemos saber, por ejemplo, si son paralelas. Es decir, no se cruzan en ningún punto. En este caso, la pendiente (m) en ambas ecuaciones debería ser la misma, siendo distinto solo el punto en el que cortan los ejes X e Y.

Asimismo, si las rectas no son paralelas, siempre se puede hallar el punto en el que se cruzan (a menos que sean rectas coincidentes o idénticas).

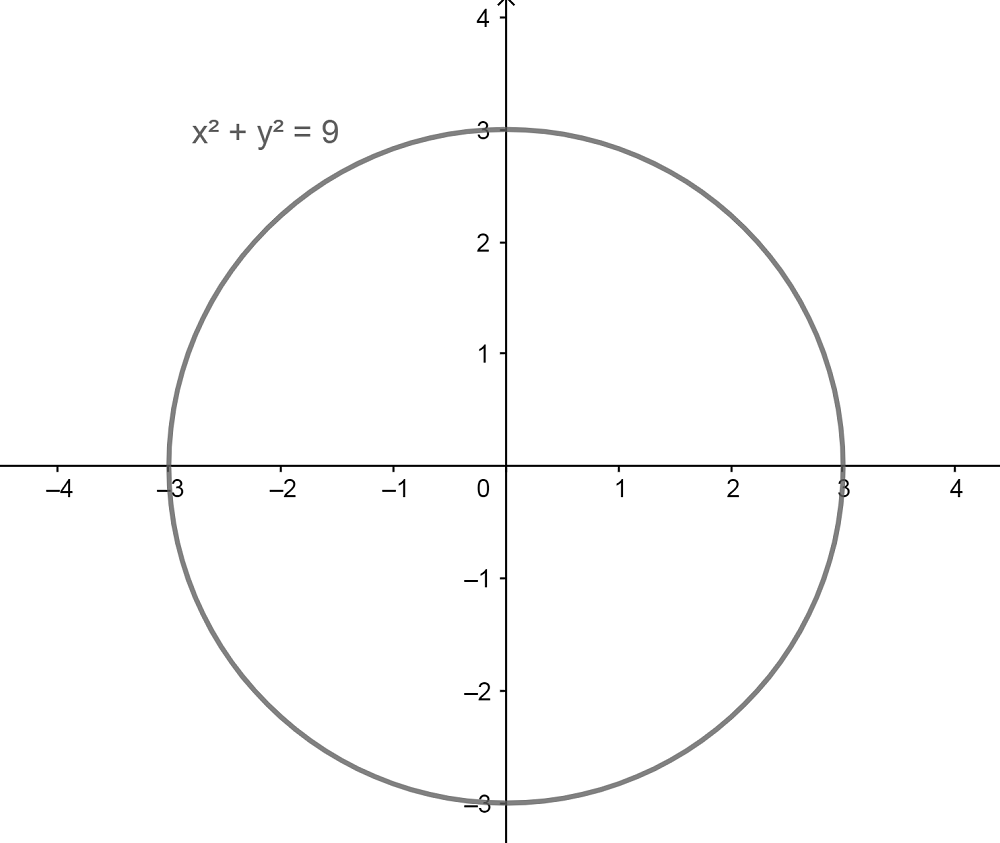
Otro tipo de figuras geométricas que pueden describirse mediante ecuaciones son los círculos. En este caso tendremos una ecuación de segundo grado, como la siguiente:

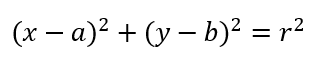
Para explicar la ecuación de arriba, consideremos que su centro es el punto (a,b) del plano cartesiano. Asimismo, cualquiera de los puntos de la circunferencia está en la coordenada (x,y), y el radio de la figura es r.

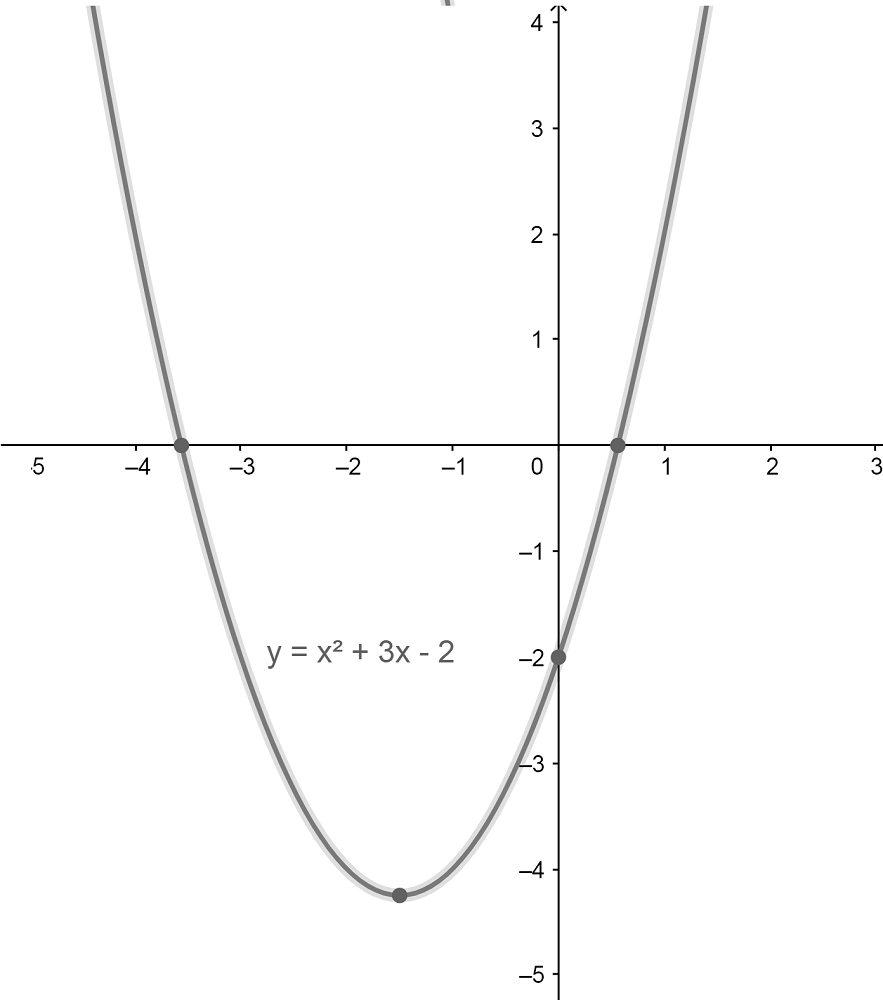
En esta línea, las parábolas tienen la siguiente forma: y = ax² + bx + c.