Estimación de máxima verosimilitud y GARCH
La Estimación de Máxima Verosimilitud (EMV) y el modelo GARCH son dos herramientas econométricas muy empleadas para hacer predicciones sobre el grado de dispersión de una muestra dado un período de tiempo a través de una autoregresión.
En otras palabras, tanto EMV y GARCH se emplean conjuntamente para encontrar el promedio de volatilidad a medio plazo de un activo financiero mediante una autorregresión.
Artículos recomendados: modelo autorregresivo (AR), GARCH y EMV.
GARCH
Fórmula Modelo GARCH (p,q):
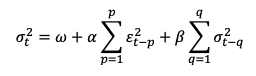
Donde
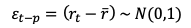
Coeficientes
Los coeficientes del modelo GARCH (p,q) son
- La constante
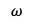
junto con
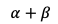
determinan el nivel promedio de volatilidad a medio plazo. Restringimos la constante a valores mayores a 0, es decir, (a+b) > 0.
- El parámetro de error
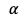
determina la reacción de la volatilidad delante sacudidas de mercado. Entonces, si este parámetro es mayor a 0,1, nos indica que la volatilidad es muy sensible cuando hay alteraciones en el mercado. Restringimos el parámetro de error a valores mayores de 0, es decir, a > 0.
- El parámetro
determina en qué cantidad se acerca la volatilidad actual a la volatilidad promedio a medio plazo. Entonces, si este parámetro es mayor a 0,9 significa que el nivel de volatilidad permanecerá después de una sacudida en el mercado.
- Restringimos
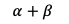
a ser menor a 1, es decir, (a+b) < 1.
Importante
Aunque estos coeficientes de obtengan mediante EMV dependen indirectamente de las características de la muestra. Entonces, si una muestra está compuesta por rentabilidades diarias, obtendremos unos resultados distintos a una muestra compuesta por rentabilidades anuales.
EMV
La EMV maximiza la probabilidad de los parámetros de una función de densidad cualquiera que depende de la distribución de probabilidad y las observaciones de la muestra.
Entonces, cuando queremos obtener una estimación de los parámetros del modelo GARCH, utilizamos la función logarítmica de máxima verosimilitud. En el modelo GARCH suponemos que la perturbación sigue una distribución normal estándar de media 0 y varianza:
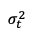
Entonces, deberemos aplicar logaritmos a la función de densidad de una distribución normal y encontraremos la función de máxima verosimilitud.
Procedimiento
- Escribir la función de densidad. En ese caso, de la distribución de probabilidad normal.
Si derivamos la función de densidad respecto a sus parámetros, encontramos las condiciones de primer orden (CPO):
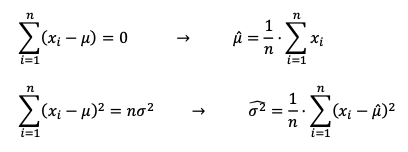
¿Encontráis familiares las fórmulas de la derecha? Son la famosa media y la varianza muestral. Estos son los parámetros de la función de densidad.
- Aplicamos logaritmos naturales:
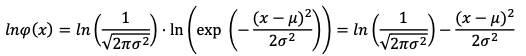
- Arreglamos la función anterior:
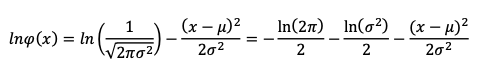
- Para obtener estimaciones de máxima verosimilitud de los parámetros anteriores, deberemos:
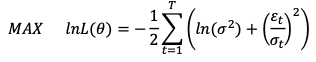
En otras palabras, para encontrar estimaciones de los parámetros de GARCH con máxima probabilidad deberemos maximizar la función de máxima verosimilitud (función anterior).
Aplicación
¿Todas las veces que queramos encontrar la función logarítmica de máxima verosimilitud tendremos que hacer los pasos anteriores? Depende.
Si suponemos que la frecuencia de las observaciones puede aproximarse satisfactoriamente a una distribución de probabilidad normal estándar, entonces, solo tendremos que copiar la última función.
Si suponemos que la frecuencia de las observaciones puede aproximarse satisfactoriamente a una distribución t de Student, tendremos que estandarizar los datos y aplicar logaritmos a la función de densidad de la t de Student. En conclusión, realizar todos los pasos anteriores.
