Modelo autorregresivo (AR)

Los modelos autorregresivos, como bien dice su nombre, son modelos que se regresan en sí mismos. Es decir, la variable dependiente y la variable explicativa son la misma con la diferencia que la variable dependiente estará en un momento del tiempo posterior (t) al de la variable independiente (t-1). Decimos ordenados cronológicamente porque actualmente nos encontramos en el momento (t) del tiempo. Si avanzamos un período nos trasladamos a (t+1) y si retrocedemos un período nos vamos a (t-1).

Dado que queremos hacer una proyección, la variable dependiente deberá estar siempre como mínimo en un período de tiempo más avanzado que el de la variable independiente. Cuando queremos hacer proyecciones mediante autorregresión, nuestra atención debe centrarse en el tipo de variable, la frecuencia de sus observaciones y el horizonte temporal de la proyección.

Popularmente se conocen como AR(p), donde p recibe la etiqueta de ‘orden’ y equivale al número de períodos los cuales vamos a retroceder para llevar a cabo el pronóstico de nuestra variable. Tenemos que tener en cuenta que cuantos más períodos retrocedamos o cuantos más órdenes adjudicamos al modelo, más información potencial figurará en nuestro pronóstico.

En la vida real encontramos previsiones mediante autorregresión en la proyección de ventas de una compañía, pronóstico sobre crecimiento del producto interior bruto (PIB) de un país, previsión sobre presupuesto y tesorería, etc.

Mayoritariamente la población asocia los pronósticos al método de Mínimos Cuadrados Ordinarios (MCO) y el error de pronóstico a los residuos de MCO. Esta confusión puede traer serios problemas cuando sintetizamos la información que nos aportan las rectas de regresión.

Diferencia en resultado:

• Estimación: Los resultados obtenidos por el método de MCO están calculados mediante observaciones presentes en la muestra y se han utilizado en la recta de regresión.
• Pronóstico: Los pronósticos se basan en un período de tiempo (t+1) avanzado al período de tiempo de las observaciones de la regresión (t). Los datos reales del pronóstico de la variable dependiente no figuran en la muestra.

Diferencia en el error:

• Estimación: los residuos (u) obtenidos por el método de MCO son la diferencia entre el valor real de la variable dependiente (Y), Y_it, y el valor estimado de (Y) dado por las observaciones de la muestra, Ý_it.

u_it = Y_it – Ý_it

El subíndice it representa la observación i-ésima en el periodo t.

• Pronóstico: El error de pronóstico es la diferencia entre el valor futuro (t+1) de (Y), Y_it+1, y la previsión para (Y) en el futuro (t+1), Ý_it+1. El valor real de (Y) para (t+1) no pertenece a la muestra.

Error pronóstico = Y_it+1 – Ý_it+1

En resumen, dos detalles a tener en cuenta:

1. Las estimaciones y los residuos pertenecen a observaciones que están dentro de la muestra.
2. Los pronósticos y sus errores pertenecen a observaciones que están fuera de la muestra.

Si queremos hacer un pronóstico sobre el precio de los forfaits para finales de esta temporada (t) basándonos en los precios de la temporada pasada (t-1), podemos utilizar el modelo autoregresivo.

Nuestra regresión autoregresiva sería:

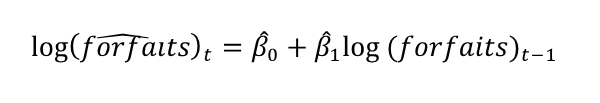
Este modelo autorregresivo pertenece a los modelos de autorregresión de primer orden o más comúnmente llamados AR(1). El significado de autoregresión radica en que la regresión se hace sobre la misma variable forfaits pero en distinto período de tiempo (t-1 y t). De la misma manera, forfaits_t no figura en la muestra forfaits_t-1.

Por concluir, la interpretación sería tal que así. Si el precio de los forfaits aumentó un 1% en el periodo anterior, cabe esperar que en el periodo siguiente aumente en B1%.