Distribución de probabilidad acumulada

En otras palabras, la distribución de probabilidad acumulada es una función matemática que se emplea para saber la probabilidad de que una variable aleatoria tome valores más pequeños o iguales que un número en concreto, sea cual sea su distribución.

La distribución de probabilidad acumulada también recibe el nombre de función de distribución (FD) y acostumbra a denotarse como F(x) para diferenciarla de la función de densidad f(x).

Es importante entender por qué en estadística se usa tanto la palabra distribución. Se emplea la palabra distribución dado que realmente se están distribuyendo los datos. Es decir, a partir de una tabla con datos se hace un gráfico para ver su apariencia. El objetivo del gráfico es ver cómo se distribuyen esos datos a lo largo de toda la muestra. La función que aparece si representamos los datos y su frecuencia sería la función de densidad de una distribución en concreto.

En cambio, si queremos representar la probabilidad acumulada de los datos, tendríamos que emplear la función de distribución o la distribución de probabilidad acumulada. 

Tal y como muestra la imagen, se puede ver como se distribuye la probabilidad (eje vertical) a través de los datos (eje horizontal). A medida que se va avanzando en la muestra, también se avanza en la probabilidad. 

Este ejemplo es una muestra de 1000 elementos que empiezan en 7 y terminan en 17:

Es importante recordar que la probabilidad siempre será un valor comprendido entre 0 y 1. Entonces, es lógico que la función de distribución de probabilidad empiece en 0 al inicio de la muestra y termine en 1 al final de la muestra. 

La función de distribución anterior hace referencia a la distribución Normal. Otras distribuciones como la Poisson, la log-normal y la exponencial también tienen una función de distribución parecida. 

Sitúa en la siguiente gráfica las siguientes probabilidades: 

1. 40%
2. 20%
3. 90%

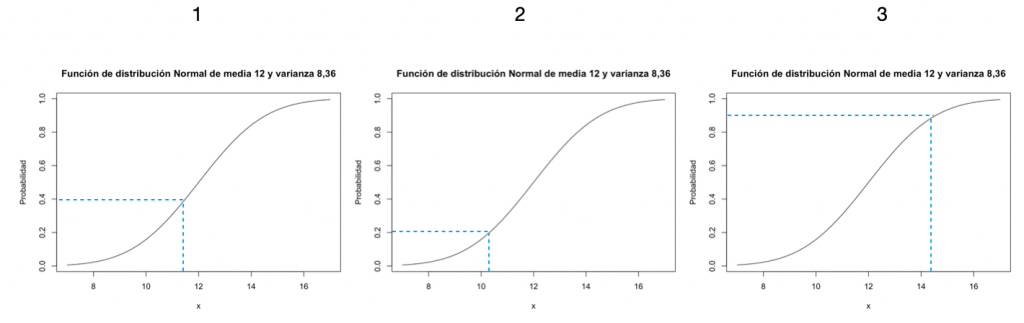
A diferencia de la función de densidad de probabilidad, en la función de distribución las probabilidades son puntos de la curva y no áreas. Este ejercicio se podría plantear también sabiendo la observación (eje horizontal) y buscar la probabilidad asociada.