Distancia entre dos puntos
La distancia entre dos puntos de dimensión R en el espacio es la aplicación de la raíz cuadrada al vector que forman esos puntos ordenados.
En otras palabras, la distancia entre dos puntos en el espacio es el módulo del vector formado por dichos puntos.
La distancia entre dos puntos no es nada más que el módulo del vector que forman los puntos dados. Una vez calculado el módulo del vector, ya tendremos la distancia entre los dos puntos.
Fórmula
Dados los siguientes dos puntos:
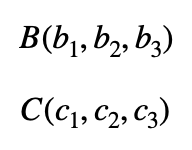
Entonces, la distancia entre estos dos puntos será el módulo del vector que forman:
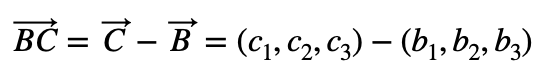
Por lo tanto, el módulo de este vector será la distancia entre estos dos puntos:
La longitud de la raíz dependerá del número de dimensiones que tengan los puntos. Si son puntos de solo dos dimensiones, solo habrá dos términos dentro de la raíz. En cambio, si los puntos tienen 6 dimensiones, entonces, habrá 6 elementos dentro de la raíz.
Se dice que los puntos tienen que estar ordenados porque en los vectores, al igual que en las matrices, el orden de los factores sí importa y es crucial para solucionar correctamente los problemas. No es lo mismo un vector que va desde el punto B hacia el punto C que otro vector que va desde el punto C hacia el punto B.
De forma esquemática:
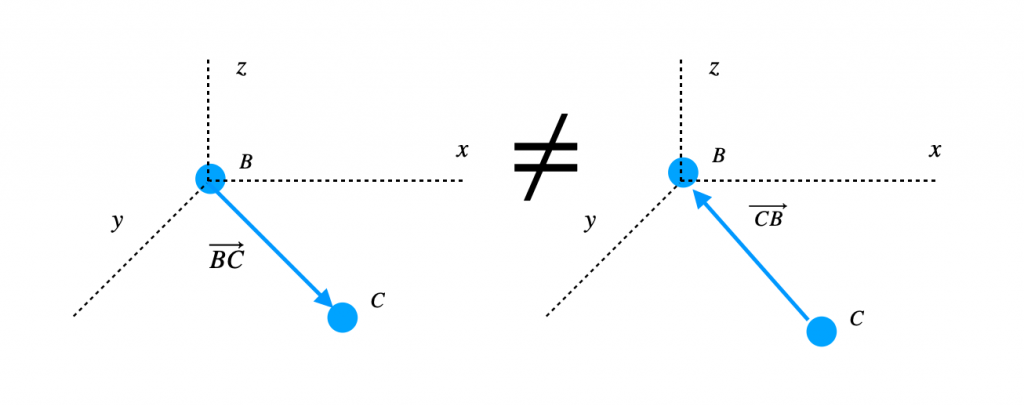
Lo que comparten los dos vectores anteriores es la distancia: tanto el vector BC como el vector CB conservan la misma distancia entre sus puntos. En otras palabras, tienen el mismo módulo.
Esto se debe a que la diferencia de los dos vectores es únicamente el signo de sus coordenadas. Dado que el módulo incluye hacer el cuadrado de las coordenadas del vector, produce el mismo efecto que si aplicásemos el valor absoluto. De hecho, este es el motivo por el cual indicamos el módulo de un vector con las dos líneas paralelas:
Luego se aplica la raíz para quitar el efecto del cuadrado de los componentes y volver a las mismas unidades.
Distancia en geometría analítica y en la realidad
Cuando tengamos que calcular distancias en geometría analítica podemos ayudarnos con ejemplos reales. Por ejemplo, si nos piden calcular la distancia entre dos puntos, como en este caso, nos podemos imaginar nosotros como punto inicial (punto B) y un objeto como punto final (punto C). Entonces, podemos medir esa distancia haciendo la resta en valor absoluto entre un punto y el otro. En otras palabras más técnicas, calcular el módulo.
Veremos que desde nuestra posición hacia el objeto y desde el objeto hacia nosotros existirá la misma distancia. Además, esa distancia siempre será positiva, sea 0 o mayor. Puede ser que estemos sujetando el objeto y, por tanto, esa distancia sea 0, o que el objetivo esté alejado, por tanto, una distancia positiva.
Ejemplo de distancia entre dos puntos
Calcula la distancia entre los siguientes puntos:


 José Antonio Ludeña
José Antonio Ludeña