Diferencia entre cóncavo y convexo

Así, podemos describirlo de otra manera. La parte central de una superficie cóncava está más hundida o deprimida. En cambio, si fuera convexa, esa parte central mostraría una prominencia.

Para entenderlo mejor podemos citar algunos ejemplos. Primero, el clásico caso de una esfera, cuya superficie es convexa. Sin embargo, si la cortáramos en dos y nos quedáramos con la mitad inferior, tendríamos un objeto cóncavo, con un hundimiento (suponiendo que el interior de la esfera está vacío).

Otro ejemplo de convexo sería una montaña, pues es una prominencia respecto a la superficie terrestre. Por el contrario, un pozo es cóncavo, pues entrar en él implica hundirse, por debajo del nivel de la superficie terrestre.

Cabe destacar, además, que para definir a un objeto como cóncavo o convexo también se debe tener en cuenta la perspectiva. Así, un plato de sopa, por ejemplo, cuando está dispuesto para servir, es cóncavo, tiene un hundimiento. Sin embargo, si lo volteamos, el plato será convexo.

Por otro lado, en el caso de las las parábolas, estas son convexas si tienen forma de U, pero cóncavas si presentan una forma de U invertida.

Si la segunda derivada de una función es menor que cero en un punto, entonces la función es cóncava en ese punto. En cambio, si es mayor a cero, es convexa en ese punto. Lo anterior puede expresarse de la siguiente forma:

Si f»(x)<0, f(x), esta es cóncava.

Si f»(x)>0, f(x) esta es convexa.

Por ejemplo, en la ecuación f(x)=x²+5x-6, podemos calcular su primera derivada:

f''(x)=2x+5

Luego, hallamos la segunda derivada:

f»(x)=2

Por lo tanto, como f»(x) es mayor a 0, la función es convexa para todo valor de x, como vemos en el gráfico inferior:

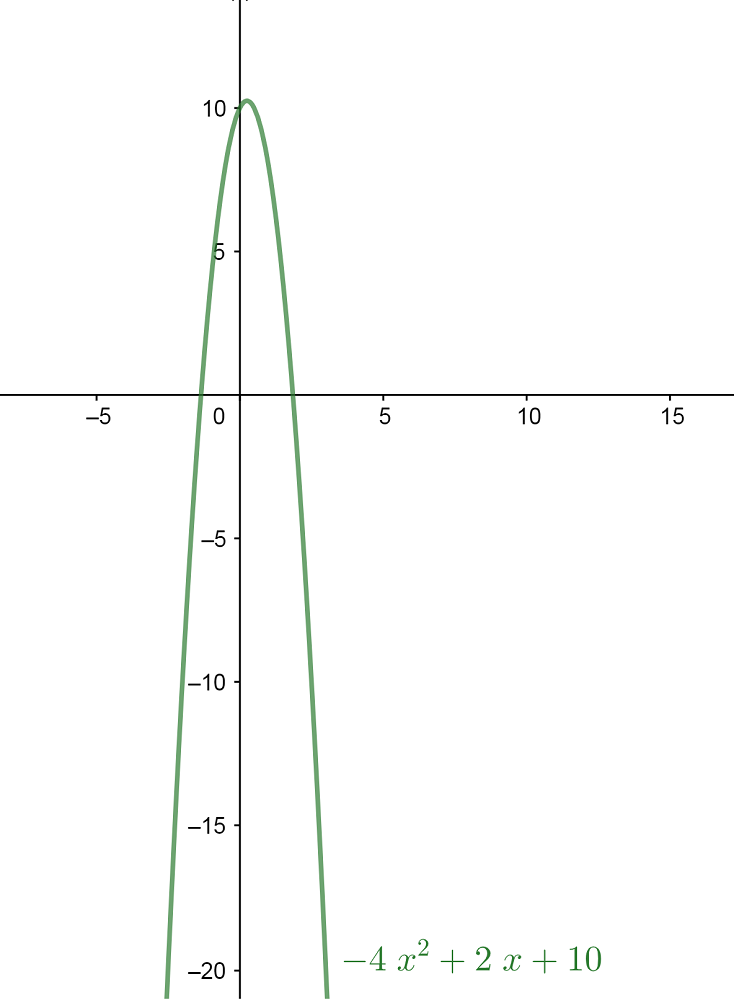
Ahora, veamos el caso esta otra función: f(x)=-4x²+7x+9.

f''(x)=-8x+7

f»(x)=-8

Por lo tanto, como la segunda derivada es menor a 0, la función es cóncava para todo valor de x.

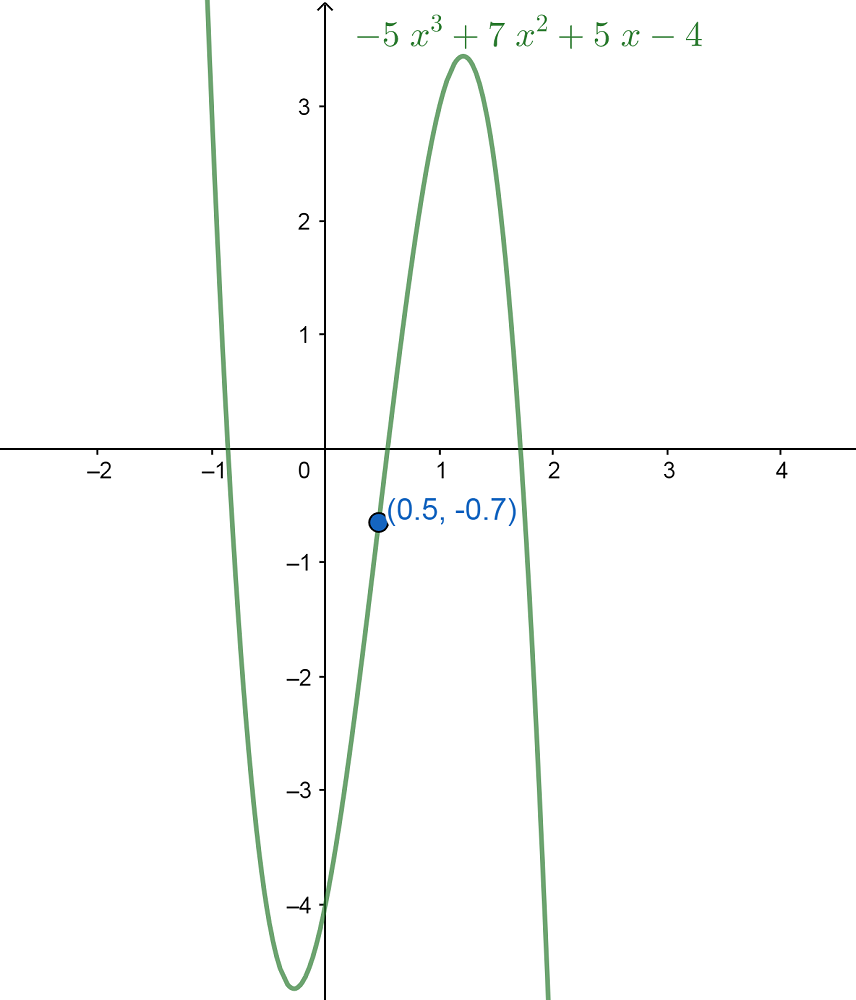
Pero ahora observemos la siguiente ecuación: -5 x³+7x²+5 x-4

f''(x)=-15x²+14x+5

f»(x)=-30x+14

Igualamos la segunda derivada a cero:

-30x+14=0

x=0,4667

Entonces, cuando x es mayor a 0,4667, f»(x) es mayor a cero, por lo que la función es convexa. Mientras que si x es menor a 0,4667, la función es cóncava, como vemos en el gráfico inferior:

Un polígono convexo es aquel donde se pueden unir dos de sus puntos, trazando una línea recta que se mantiene dentro de la figura. Asimismo, sus ángulos interiores son todos menores a 180º.

En cambio, un polígono cóncavo es aquel donde, para unir dos de sus puntos, se debe trazar una línea recta que está fuera de la figura, siendo esta una diagonal exterior que une dos vértices. Además, al menos uno de sus ángulos interiores es mayor a 180º.

Podemos observar una comparación en la imagen que se ofrece a continuación: