Baricentro de un triángulo
El baricentro de un triángulo es el punto en el que se cruzan las medianas de la figura. También se le conoce como centroide.
Cabe recordar que la mediana es aquel segmento que une el vértice del triángulo con el punto medio de su lado opuesto. Así, cada triángulo tiene tres medianas.
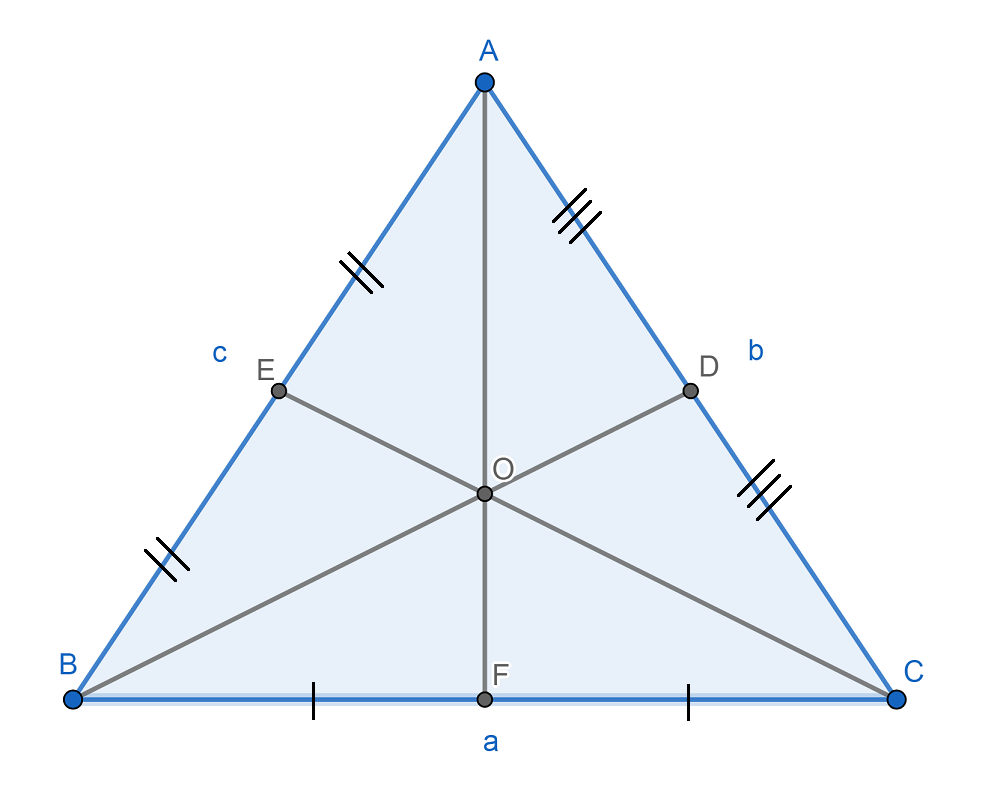
Por ejemplo, en el triángulo de arriba, el baricentro es el punto O, siendo las medianas los segmentos AF, BD y CE.
Una propiedad importante del baricentro es que su distancia respecto a cada vértice es dos veces la distancia respecto al lado contrario.
Para explicarlo mejor, en cada mediana se pueden distinguir dos partes:
- La distancia del vértice al baricentro, que es 2/3 de la longitud de la mediana
- El 1/3 restante, que es la distancia del baricentro al punto medio del lado opuesto.
En la imagen superior, por ejemplo, se cumple que:
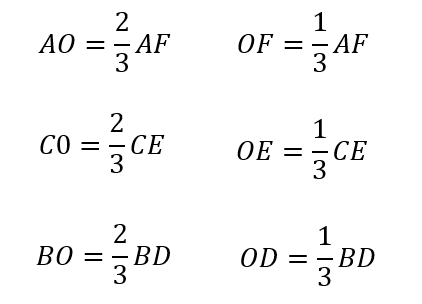
Cómo hallar el baricentro de un triángulo
Para hallar el baricentro del triángulo debemos tomar en cuenta que, conociendo los coordenadas de los tres vértices del triángulo, las coordenadas del baricentro corresponden a su media aritmética. Entonces, supongamos que los vértices son:
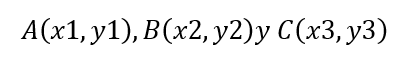
Entonces, las coodenadas del baricentro, que llamaremos O, serían:
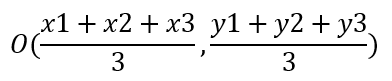
Ahora, también es posible hallar el baricentro si contamos con las ecuaciones de las rectas que contienen, al menos, dos de las medianas.
Recordemos que en la geometría analítica, se puede expresar una recta como una ecuación algebraica de primer orden como:
y = xm+b
En la ecuación mostrada, y es la coordenada en el eje de las ordenadas (vertical), x es la coordenada en el eje de las abscisas (horizontal), m es la pendiente (inclinación) que forma la recta respecto al eje de las abscisas, y b es el punto en el que la recta corta el eje de las ordenadas.
Para entender mejor lo anterior, veamos un ejemplo.
Ejemplo de baricentro
Supongamos que tenemos un triángulo del cual conocemos dos de sus vértices:
A(0;4) y B(-2;1)
Ahora, se sabe además que el punto medio del lado opuesto al vértice A es (3;1), y el punto medio del lado opuesto al vértice B es (4;2,5). Vale aclarar que estamos usando el punto y coma para no confundir con la coma que separa los decimales.
Primero hallaremos la ecuación de la recta que contiene la mediana que parte del vértice A, tomando en cuenta que la pendiente cuando se pasa de un punto a otro debe ser siempre la misma. La pendiente es la variación en el eje vertical entre la variación en el eje horizontal:
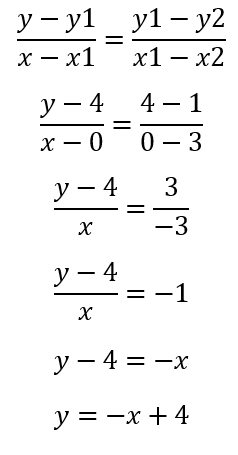
Lo que hemos hecho es asumir que la recta pasa por un punto (x1;y1), que es el vértice A (0;4), y por el punto (x2;y2) que es el punto medio de su lado opuesto (3,1).
Luego, hacemos lo mismo con el vértice B (-2;1) y el punto medio de su lado contrario(-4;-2,5):
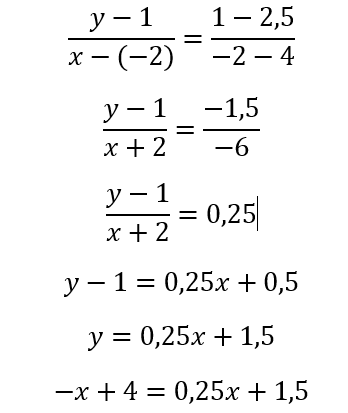
Paso siguiente, igualamos el lado derecho de las dos ecuaciones halladas para despejar el valor en el eje X cuando ambas coinciden:
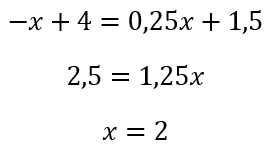
Luego despejamos en cualquiera de las ecuaciones para hallar el valor de y:
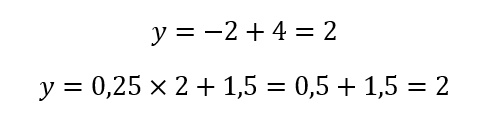
Por lo tanto, el baricentro del triángulo es el punto (2,2) en el plano cartesiano.
