Apotema
La apotema es la distancia más pequeña que puede notarse entre el centro de la figura y cualquiera de sus lados, siendo representada a través de un segmento.
En el caso de un polígono regular (aquel que tiene todos sus lados y ángulos interiores de la misma medida), la apotema tiene como extremos el centro de la figura y el punto medio de cualquiera de sus lados.
Es decir, en el polígono regular, la intersección entre la apotema y el lado de la figura geométrica determina la división del lado en dos partes iguales.
Asimismo, la apotema y el lado del polígono regular son perpendiculares, es decir, al cruzarse forman cuatro ángulos rectos o de 90º.
Como podemos ver en la figura de abajo, además, la apotema (que es el segmento FG) es el centro de la circunferencia circunscrita del polígono, es decir, que lo contiene.
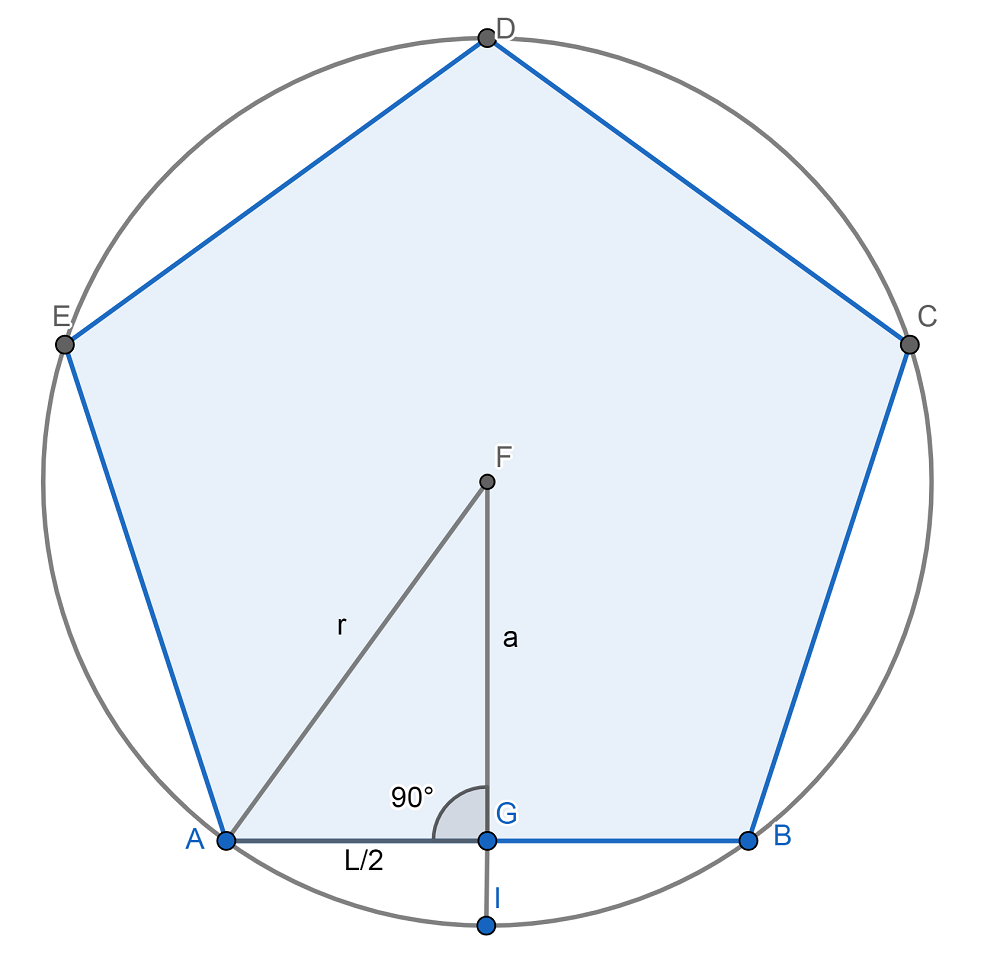
Por ejemplo, en la imagen de arriba, la apotema es el segmento FG, mientras que al segmento GI se le conoce como sagita.
Un dato adicional a tener en cuenta es que la apotema en una figura tridimensional como la pirámide es el segmento que une el vértice con el punto medio de cualquiera de los lados que conforman la base del poliedro.
Fórmula de la apotema
La fórmula de la apotema puede ser calculada, en el caso de un polígono regular, tomando como referencia el teorema de Pitágoras.
Observemos de nuevo la figura de arriba, el segmento FG es la apotema, y el segmento AG es la mitad del lado del polígono. Asimismo, el segmento FA es el radio de la circunferencia circunscrita a la figura.
Entonces, tenemos un triángulo rectángulo donde la hipotenusa es el radio de la circunferencia circunscrita (r), mientras que los catetos son la apotema (a) y el segmento AG que mide la mitad del lado (L/2).
Luego, recordando el teorema de Pitágoras, la hipotenusa al cuadrado es igual a la suma de cada uno de los catetos elevado al cuadrado. Luego, despejamos la apotema.
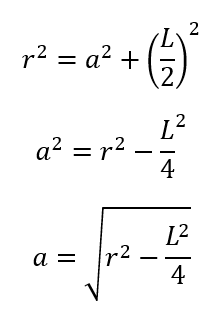
Vale precisar que esta fórmula es para calcular la apotema de un polígono regular.
Ejemplo de apotema
Supongamos que tenemos un polígono que está inscrito en una circunferencia con un radio que mide 17 metros. Asimismo, el lado de la figura mide 20 metros. ¿Cuál es la longitud de la apotema de la figura?
La apotema de este polígono es de 13,7477 metros.
