Definición de tautología
 Tautología es un término que proviene de un vocablo griego y que hace referencia a la repetición de un mismo pensamiento a través de distintas expresiones. Una tautología, para la retórica, es una afirmación redundante.
Tautología es un término que proviene de un vocablo griego y que hace referencia a la repetición de un mismo pensamiento a través de distintas expresiones. Una tautología, para la retórica, es una afirmación redundante.
Es habitual que las tautologías sean consideradas como un error en el lenguaje o una falta de estilo. Sin embargo, es posible apelar a las tautologías para enfatizar una cierta idea. Por ejemplo: la oración “Puedo confirmar que el acusado es culpable ya que vi el asesinato con mis propios ojos” presenta una aclaración innecesaria acerca del uso de sus ojos, dado que no podría haber visto por otro medio; del mismo modo, el énfasis de la palabra «propios» puede omitirse absolutamente.
Otros ejemplos muy comunes de tautología se pueden apreciar en las siguientes oraciones: “Voy a subir arriba a buscar un libro y vuelvo”, “Tengo que salir afuera para regar las plantas”. Siempre que se sube es hacia arriba; del mismo modo, salir implica trasladarse fuera de un lugar, por lo cual dichas aclaraciones carecen de sentido y resultan innecesarias para la comprensión.
Cuando la tautología supone una explicación redundante que no aporta un nuevo conocimiento, se suele hablar de perogrullada o verdad de Perogrullo: “Soy lo que soy”. La expresión en la que aparecen términos redundantes (como “subir arriba” o “salir afuera”), por otra parte, recibe el nombre de pleonasmo.
En el ámbito de la lógica, una tautología es una fórmula de un sistema que resulta verdadera para cualquier interpretación. En otras palabras, se trata de una expresión lógica que es verdadera para todos los posibles valores de verdad de sus componentes atómicos. Para saber si una fórmula dada es una tautología, se debe construir una tabla de verdad.
Tabla de verdad
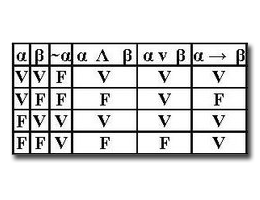 La tabla de verdad (también conocida como tabla de valores de verdad) presenta una proposición compuesta y su valor de verdad para cada una de las combinaciones posibles que se puedan dar con sus elementos. Su autor fue el filósofo y científico norteamericano Charles Sanders Peirce, también conocido como el máximo representante de la semiótica moderna, y la publicó a mediados de 1880.
La tabla de verdad (también conocida como tabla de valores de verdad) presenta una proposición compuesta y su valor de verdad para cada una de las combinaciones posibles que se puedan dar con sus elementos. Su autor fue el filósofo y científico norteamericano Charles Sanders Peirce, también conocido como el máximo representante de la semiótica moderna, y la publicó a mediados de 1880.
Para configurar un sistema formal, es necesario establecer las definiciones de cada operador y los argumentos deben ser expuestos en forma de razonamientos deductivos lógico-lingüísticos, responder a un diseño puramente matemático y constituir una aplicación lógica que defina sus variables de entrada y salida.
Los dos posibles valores que puede arrojar una tabla de verdad son: verdadero, el cual se expresa mediante la letra «V» o con el número «1» e indica que el el circuito se encuentra cerrado; falso, representado por la letra «F» o el número «0», cuando un circuito se encuentra abierto. Las proposiciones a analizar son las variables, y se ubican en la parte superior de la tabla, ocupando el lugar que comúnmente se destina a los nombres de campos.
Los operadores utilizados en una tabla de verdad son:
* negación: al ejecutarlo sobre un valor de verdad determinado, arroja el opuesto (si originalmente era verdadero, devuelve falso, y viceversa);
* conjunción: se utiliza para operar con dos valores de verdad, generalmente de dos proposiciones diferentes, y devuelve verdadero cuando las dos lo son, y falso para el resto de los casos;
* disyunción: similar a la conjunción, pero le basta que una de las dos proposiciones tenga valor verdadero para devolver tal resultado;
* condicional: también conocido por el nombre de implicación, toma dos proposiciones y arroja falso solamente cuando la primera devuelve verdadero y la segunda, falso. Para los casos restantes, su resultado es verdadero;
* bicondicional: opera sobre los valores de verdad de dos proposiciones y devuelve verdadero si ambas tienen el mismo valor y falso en el caso contrario.
