Definición de polígono estrellado
Un polígono es una figura compuesta por una cierta cantidad de lados, que son segmentos no alineados y rectos. Dependiendo de sus características, existen múltiples clasificaciones de los polígonos.
Los polígonos cóncavos son aquellos que tienen, al menos, un ángulo interior que mide más de 180° o de pi radianes. Dentro de este grupo, se encuentran los polígonos estrellados, caracterizados por su forma de estrella.
Un polígono estrellado, por lo tanto, es cóncavo ya que cuenta con uno o más ángulos interiores de más de 180° o pi radianes. Otras características propias de los polígonos cóncavos y de los polígonos estrellados son que, además, tienen una o más diagonales exteriores y disponen de dos o más vértices que, al ser unidos por un segmento, éste corta al menos un lado de la figura.
Un polígono estrellado no sólo es cóncavo, sino que también puede formar parte de los polígonos regulares cuando sus ángulos interiores y sus lados son iguales. A través de ciertas “uniones” realizadas mediante nuevos segmentos que vinculen los vértices, se puede crear un polígono estrellado a partir de un polígono regular (como un pentágono, por ejemplo).
Los polígonos estrellados regulares, además, pueden ser simples. Esto ocurre cuando sus vértices se encuentran, de manera alternativa, sobre un par de circunferencias concéntricas y con ángulos centrales que resultan iguales.
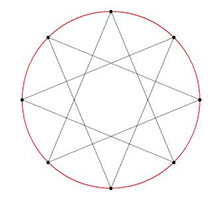
Una manera de construir polígonos estrellados es mediante la superposición y el giro de otros polígonos. Así es posible desarrollar numerosos polígonos con forma de estrella, como la famosa Estrella de David, que es un símbolo de la religión judía.
Al dividir una circunferencia en n partes y unirlas de manera sucesiva es posible obtener un polígono regular convexo; si las uniones entre los vértices se efectúan de dos en dos, de tres en tres, etcétera, se obtiene un polígono cóncavo y estrellado. En otras palabras, para construir un polígono estrellado se puede partir de uno regular convexo y unir sus vértices en secuencia continua manteniendo el intervalo entre uno y otro, de manera que se cumplan las siguientes condiciones:
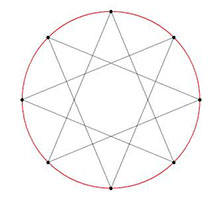* el número de vértices del polígono original (N) sobre el espacio entre uno y otro (M) debe formar una fracción irreducible, o sea, que su denominador y su numerador no tengan factores en común, por lo cual la fracción no pueda simplificarse;
* el polígono estrellado que se forma uniendo los vértices de un polígono regular convexo debe ser el mismo independientemente del sentido en el cual se tracen los segmentos. En otras palabras, N/M y N/(N-M) deben representar al mismo polígono.
Algunos conceptos relacionados con el polígono estrellado son los siguientes: género, la cantidad de lados (o cuerdas) que posee, la cual debe coincidir con su número de vértices, razón por la que su denominación es igual a la de los polígonos convexos (con un género 6 se habla de hexágono estrellado, por ejemplo); paso, la cantidad de partes en las cuales se divide la circunferencia, y el valor que comprende los lados del polígono; especie, una propiedad con denominación ordinal que hace referencia al paso, tal que si las uniones son de dos en dos se habla de segunda especie, y así sucesivamente.
De los polígonos más conocidos, se sabe que el triángulo y el cuadrado no tienen uno estrellado; el pentágono, el octógono, el decágono y el dodecágono, por otro lado, tienen uno cada uno, de primera, segunda, segunda y de quinta o cuarta especie, respectivamente; el heptágono y el eneágono tienen dos cada uno, de primera y segunda especie; el de once lados, por último, tiene cuatro, que van de primera a cuarta especie.