Definición de paralelepípedo
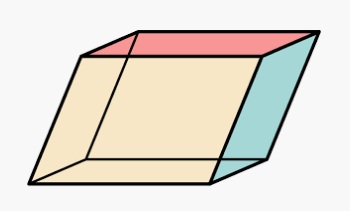 El vocablo griego parallēlepípedon derivó en el latín tardío parallelepipĕdum, que es el antecedente etimológico más cercano de paralelepípedo: un cuerpo geométrico que se encuentra limitado por seis paralelogramos y que tiene sus caras opuestas paralelas e iguales.
El vocablo griego parallēlepípedon derivó en el latín tardío parallelepipĕdum, que es el antecedente etimológico más cercano de paralelepípedo: un cuerpo geométrico que se encuentra limitado por seis paralelogramos y que tiene sus caras opuestas paralelas e iguales.
Cabe destacar que, en geometría, un cuerpo o sólido es un objeto que presenta las tres dimensiones más importantes (altura, anchura y longitud). En el caso específico del paralelepípedo, se trata de un poliedro: un cuerpo formado por superficies planas.
Los paralelepípedos, en definitiva, son hexaedros (poliedros que tienen seis caras). La totalidad de sus caras son paralelogramos (cuadriláteros con sus lados opuestos paralelos e iguales); entre los paralelogramos del paralelepípedo, aquellos que se oponen entre sí son idénticos y paralelos.
Cada paralelepípedo cuenta con ocho vértices y doce aristas. Como los vértices se disponen en un par de planos paralelos, el paralelepípedo es un prismatoide. Las aristas, por su parte, son paralelas e iguales en grupos de a cuatro.
De acuerdo a sus características, es posible diferenciar entre distintos tipos particulares de paralelepípedos. El paralelepípedo cuyos paralelogramos son cuadrados recibe el nombre de cubo o hexaedro regular. El paralelepípedo formado por rombos, en tanto, es un paralelepípedo oblicuo o romboedro, mientras que el paralelepípedo constituido por rectángulos es un paralelepípedo rectangular u ortoedro. Si las seis caras del paralelepípedo son romboides, se trata de un romboiedro.
Podemos encontrar paralelepípedos en múltiples situaciones cotidianas. Un ladrillo, por mencionar un caso, es un paralelepípedo: suele presentar cuatro rectángulos (opuestos dos a dos) y dos cuadrados (también opuestos entre sí).
 Los cálculos de sus propiedades son relativamente más complejas que las de una figura de dos dimensiones, ya que el paralelípedo tiene tres; sin embargo, como suele suceder en estos casos, se apoyan en las fórmulas del universo bidimensional como punto de partida. Tomemos por ejemplo el volumen, es decir, la magnitud que se define como la extensión tridimensional de una región: para su cálculo, en primer lugar se debe hallar el área de una de sus caras (puede ser cualquiera de ellas) y luego multiplicarla por la altura de la figura partiendo de ella.
Los cálculos de sus propiedades son relativamente más complejas que las de una figura de dos dimensiones, ya que el paralelípedo tiene tres; sin embargo, como suele suceder en estos casos, se apoyan en las fórmulas del universo bidimensional como punto de partida. Tomemos por ejemplo el volumen, es decir, la magnitud que se define como la extensión tridimensional de una región: para su cálculo, en primer lugar se debe hallar el área de una de sus caras (puede ser cualquiera de ellas) y luego multiplicarla por la altura de la figura partiendo de ella.
La fórmula que responde a dicho cálculo se expresa de la siguiente manera: V = A h, donde la V es el volumen, la A es el área y la h es la altura. Esto se usa en la mayoría de los casos, pero existe uno que simplifica considerablemente el cálculo: aquél en el que todas las caras del paralelípedo sean perpendiculares entre ellas. Para ello, basta con multiplicar su altura, anchura y longitud, partiendo de cualquiera de sus vértices y midiendo las tres aristas que convergen en él.
Dichas longitudes se representan mediante tres letras, que dan nombre a las aristas, y la fórmula resultante es la siguientes: V = w u v. Claro que existe un caso aún más simple, aunque se relaciona más con el anterior que con el primero: el cubo. No olvidemos que esta figura tiene todas sus aristas de igual extensión, así como el cuadrado tiene cuatro lados idénticos. En este caso, basta con elevar al cubo dicha extensión: V = l3.
Por otra parte podemos afirmar que si entendemos las tres aristas que se encuentran en un mismo vértice son tres vectores, entonces para calcular su volumen podemos hallar el producto mixto y luego, su valor absoluto: V = |a . (b x c)|. Esto nos demuestra que el modo de estudiar una misma figura geométrica depende de sus características particulares, pero también de las necesidades, los conocimientos y las preferencias de la persona. Al trasladar esto a un ordenador, la elección de un método u otro a veces depende de cuán exigente resulte para el procesador.
