Definición de ortocentro
La noción de ortocentro se emplea en el ámbito de la geometría. Así se denomina al punto donde las alturas de un triángulo se cruzan.
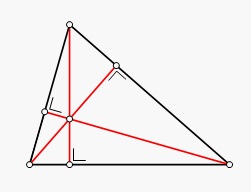 Es importante señalar que cada triángulo tiene tres alturas. Estas alturas son las rectas que permiten unir un vértice con su lado opuesto, siendo perpendiculares a dichos lados.
Es importante señalar que cada triángulo tiene tres alturas. Estas alturas son las rectas que permiten unir un vértice con su lado opuesto, siendo perpendiculares a dichos lados.
El punto en el cual las tres alturas se cortan es el ortocentro. La ubicación del ortocentro depende de las características del triángulo.
En un triángulo obtusángulo (que dispone de un ángulo obtuso y dos agudos), el ortocentro se encuentra afuera de la figura. Si el triángulo es rectángulo (tiene un ángulo recto), el ortocentro resulta coincidente con el vértice del ángulo de 90º. En el caso de los triángulos acutángulos (todos sus ángulos son agudos), el ortocentro se sitúa adentro de la figura.
Resumiendo, puede decirse que, en los triángulos, la altura es una recta que atraviesa un vértice y es perpendicular al lado opuesto. Cada uno de los triángulos cuenta con tres alturas: el punto donde se encuentran las alturas recibe la denominación de ortocentro, que puede localizarse adentro o afuera del propio triángulo.
En los triángulos equiláteros (cuyos lados miden lo mismo), el ortocentro, el circuncentro, el baricentro y el incentro coinciden en un punto interior que se halla a idéntica distancia de los tres vértices. En los triángulos no equiláteros, en cambio, el ortocentro, el circuncentro y el baricentro se posicionan alineados y comprendidos en la llamada recta de Euler. Una propiedad indica que la distancia del ortocentro al baricentro duplica la distancia que existe entre el baricentro y el circuncentro.
