Definición de momento flexor
En el ámbito de la física, se denomina momento de una fuerza a la magnitud que se obtiene al multiplicar el valor de la fuerza por la distancia que mantiene hacia un cierto punto. Según sus características, es posible reconocer diversos momentos de esta clase.
El momento flexor, también conocido como momento de flexión o momento flector, es aquel momento de fuerza que resulta de la distribución de las tensiones sobre un plano perpendicular al eje longitudinal sobre el cual se genera la flexión o sobre una pieza prismática que se encuentra flexionada.
Otra posible definición parte de los elementos lineales perpendiculares y habla de una función que recorre el eje neutro, en la cual la variable x es equivalente a la longitud sobre dicho eje. Aquí aparece otro concepto, el de eje neutro (también conocido como línea o fibra neutra), la superficie material curva de una placa o un prisma mecánico que se deforma a causa de la flexión y que separa la zona comprimida de la traccionada.
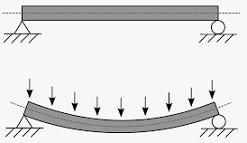
Las losas, los pilares y las vigas suelen registrar momentos flexores debido a que tienden a deformarse por flexión (dobladura o curvatura). Cuando el momento flexor genera tensiones en los sectores superiores, se trata de un momento negativo que deriva en una curvatura convexa; en cambio, si el momento flexor provoca tensiones en las zonas inferiores, se hace referencia a un momento positivo que causa una curvatura cóncava.
Cabe destacar que el momento flexor resulta nulo en el punto de inflexión. Allí la curvatura cambia de cóncava a convexa (o viceversa).
Puede afirmarse que el momento flexor es la suma, respecto a un eje, de los momentos de las fuerzas de extensión y de compresión que actúan de forma simultánea. Para simbolizar el momento flexor se apela a una letra m mayúscula: M.
La representación gráfica de los cambios en la magnitud de un momento flexor, por último, recibe el nombre de diagrama del momento flexor. En este gráfico se muestran las modificaciones que se producen a lo largo del eje cuando se registran ciertas cargas transversales y con determinadas condiciones de apoyo.
Si se cumplen las condiciones de equilibrio, el momento flexor es equivalente a la fuerza resultante de todas las que se encuentran a uno de sus dos lados, es decir que coincide con una fuerza que podría producir el mismo efecto que todas las demás juntas. Como un mismo elemento puede verse afectado a diversas cargas distribuidas, momentos y fuerzas, el diagrama de momento flexor presenta variaciones en su desarrollo.
Tomando un plano medio, si conocemos el desplazamiento vertical del eje baricéntrico que tiene lugar sobre éste, entonces podemos usar la llamada ecuación de la curva elástica para calcular el momento flexor: M(x) = d / dx (EI dy / dx), en la cual:
* M(x) es el desplazamiento, ya sea de la curva elástica o vertical; * E es el módulo de elasticidad longitudinal del material de la viga;
* I es el momento de inercia de área de la parte transversal de la viga.
En este punto es necesario definir brevemente el concepto de curva elástica. Se enmarca en una viga recta y se trata de una que se deforma por su flexión del eje longitudinal, a causa de que se apliquen cargas transversales sobre el plano xy de la misma.
El módulo de elasticidad longitudinal o de Young, por otro lado, es un parámetro que sirve para medir el comportamiento de un material elástico de acuerdo con la dirección en la que ejerza una fuerza sobre él. Fue observado por primera vez en el siglo XIX por el científico Thomas Young.