Definición de isometría
 La Real Academia Española (RAE) reconoce tres acepciones del término isometría. La primera de ellas alude a la equivalencia o correspondencia de medidas.
La Real Academia Española (RAE) reconoce tres acepciones del término isometría. La primera de ellas alude a la equivalencia o correspondencia de medidas.
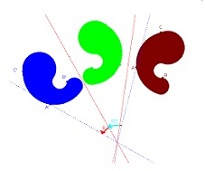
En el ámbito de la geometría, la idea de isometría refiere al vínculo establecido por dos figuras que conservan las distancias entre los puntos correspondientes. La isometría puede obtenerse a través de reflexión, rotación o traslación.
Una figura registra una transformación isométrica en un plano cuando mantiene la igualdad de medidas: es decir que el cambio solamente implica una modificación de posición, y no de tamaño o de forma. La figura inicial y la figura final, pues, son geométricamente congruentes y semejantes.
La transformación isométrica requiere el trabajo con un sistema de coordenadas. Este tipo de sistema permite el movimiento de un punto en cualquier dirección, siempre manteniéndose en el plano en cuestión.
La isometría, en este marco, es una forma de proyección que suele emplearse en el dibujo técnico para representar a escala. La proyección isométrica ayuda a representar un objeto tridimensional en dos dimensiones.
Los videojuegos han tenido una relación muy estrecha con la isometría, en especial en la época de transición entre los gráficos bidimensionales y los tridimensionales. Para explicar las razones y las técnicas usadas debemos remontarnos a los primeros títulos. Si bien existen ejemplos de aplicaciones interactivas pertenecientes a los años 60 que podrían ser consideradas videojuegos, el mayor número de productos comerciales y de alcance masivo llegó en los 80, con un arranque lento una década antes. En aquella época, los personajes y los objetos se dibujaban con píxeles, es decir, en dos dimensiones y de una forma absolutamente estática.
Un gráfico hecho con píxeles no se puede deformar infinitamente sin que exista una pérdida de calidad y definición: por eso cuando lo ampliamos o encogemos el resultado no es muy satisfactorio. Para luchar contra esta limitación surgieron los gráficos vectoriales, que dependen de cálculos matemáticos para unir pares de puntos y formar dibujos de variada complejidad. La principal desventaja que tenían era la ausencia de relleno; básicamente, se trataba de contornos. Sin embargo, como beneficio les ofreció a los desarrolladores de antaño dar sus primeros pasos en el mundo de las tres dimensiones.
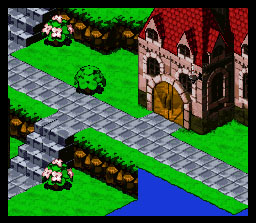 Los vectores dieron lugar a la creación de formas básicas en tres dimensiones, calculando su posición en tres ejes, pero la falta de texturas hacía que el resultado no fuera tan atractivo después del impacto inicial. No olvidemos que la industria del videojuego está formada en gran parte por artistas, tanto escritores como dibujantes y músicos, y un acabado tan hueco y poco detallado no era adecuado para dar vida a sus creaciones. Fue entonces que la isometría entró en acción.
Los vectores dieron lugar a la creación de formas básicas en tres dimensiones, calculando su posición en tres ejes, pero la falta de texturas hacía que el resultado no fuera tan atractivo después del impacto inicial. No olvidemos que la industria del videojuego está formada en gran parte por artistas, tanto escritores como dibujantes y músicos, y un acabado tan hueco y poco detallado no era adecuado para dar vida a sus creaciones. Fue entonces que la isometría entró en acción.
Cuando todavía era demasiado pronto para calcular la deformación de los objetos tridimensionales complejos y texturizados en tiempo real, algunos desarrolladores de videojuegos comenzaron a crear mundos de apariencia tridimensional con recursos bidimensionales, es decir, con gráficos hechos a base de píxeles. ¿Cómo lo consiguieron? Pues básicamente había dos caminos: crear las escenas en tres dimensiones y «fotografiarlas», para obtener los dibujos en dos dimensiones; crear directamente en píxeles las escenas teniendo en cuenta esta falsa perspectiva.
Isometría, por otra parte, es un concepto que se emplea en el ámbito de la medicina y de la educación física para nombrar a una contracción muscular que no genera que el músculo se acorte. La contracción isométrica, de este modo, implica que no se produce un acortamiento muscular: su efecto es un incremento del tono.
Los ejercicios isométricos, en este marco, consisten en tensar un músculo y hacer que se mantenga en la misma posición, conservando la tensión. Estos ejercicios son recomendados para quienes están en recuperación de una lesión que había limitado el rango de movimiento.
