Definición de fracción equivalente
 En el terreno de las matemáticas, se denomina fracción a la expresión que hace referencia a una división. La fracción 1/3, por ejemplo, implica que el número 1 se divide en 3 (o, dicho de otro modo, 1 dividido 3). Dos o más elementos equivalentes, en tanto, son semejantes o iguales.
En el terreno de las matemáticas, se denomina fracción a la expresión que hace referencia a una división. La fracción 1/3, por ejemplo, implica que el número 1 se divide en 3 (o, dicho de otro modo, 1 dividido 3). Dos o más elementos equivalentes, en tanto, son semejantes o iguales.
Para construir una fracción matemática necesitamos contar con dos componentes: un numerador y un denominador. En el párrafo anterior se menciona el ejemplo 1/3, el cual debemos leer «un tercio»; en este caso tenemos un numerador de valor 1 y un denominador que vale 3. El significado de tal dupla es que nos encontramos ante la tercera parte de un entero, una cantidad que para alcanzar la otra debe multiplicarse por tres.
Cabe mencionar que los numeradores y los denominadores siempre deben ser números enteros a excepción del cero, es decir, elementos del conjunto que tiene los números naturales desde el menos infinito hasta el más infinito. Sin ahondar en cuestiones demasiado técnicas, basta observar el concepto de fracción para entender esta regla: dado que en sí misma expresa una razón, y que el proceso de dividir su numerador por su denominador muchas veces nos da un resultado con coma, sería poco lógico construirla con números decimales.
Para leer una fracción es necesario conocer un tipo especial de palabra: el numeral. Cuando escribimos un número tenemos dos opciones: utilizar las cifras adecuadas según el sistema utilizado o bien escribir sus nombres con palabras, y para ello existen los numerales.
Los numerales son nombres propios para designar los números; en otras palabras, son sustantivos que sirven para referirse a ellos a través de la lengua escrita o hablada. Existe más de un tipo de numeral, y el uso de uno u otro depende del concepto matemático que deseemos expresar en palabras. Por ejemplo, los numerales cardinales (también conocidos por el nombre de numerales comunes) son los que usamos a diario para mencionar los números cuando necesitamos contar objetos: uno, dos, tres, etcétera.
En el caso de las fracciones, tanto de las equivalentes como de cualquier otra, se usan los numerales cardinales para hacer referencia a su numerador. Por otro lado están los numerales fraccionarios, que también se conocen como numerales partitivos, que sirven para expresar la división de un todo en varias partes: medio, tercio, cuarto, etcétera. El denominador de una fracción se lee usando estos términos.
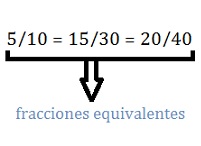
Las fracciones equivalentes, de este modo, son aquellas que, aunque se escriban de forma diferente, representan una misma cantidad. 5/10, 15/30 y 20/40, por citar algunos casos, son fracciones equivalentes. Veamos una comprobación que se obtiene mediante la división de sus numeradores por sus denominadores:
5 / 10 = 0,5
15 / 30 = 0,5
20 / 40 = 0,5
Puede afirmarse que estas fracciones (5/10, 15/30 y 20/40) son fracciones equivalentes ya que las tres señalan la misma cantidad: 0,5.
 Una manera sencilla de descubrir si dos o más fracciones resultan equivalentes consiste en multiplicar el numerador y el denominador de cada una de ellas por un mismo número. Este proceso se conoce por el nombre de amplificación.
Una manera sencilla de descubrir si dos o más fracciones resultan equivalentes consiste en multiplicar el numerador y el denominador de cada una de ellas por un mismo número. Este proceso se conoce por el nombre de amplificación.
Retomando el ejemplo anterior, podemos probar con el número 3:
(5 x 3) / (10 x 3) = 15 / 30 = 0,5
(15 x 3) / (30 x 3) = 45 / 90 = 0,5
(20 x 3) / (40 x 3) = 60 / 120 = 0,5
La simplificación es un proceso similar, aunque basado en la división del numerador y el denominador por un mismo número. Es importante señalar que para poder completar esta operación los dos términos deben ser divisibles por el número en cuestión. Si el resultado es igual, entonces estamos ante fracciones equivalentes. Podemos hacer la prueba con los ejemplos anteriores y el número 5:
(5 / 5) / (10 / 5) = 1 / 2 = 0,5
(15 / 5) / (30 / 5) = 3 / 6 = 0,5
(20 / 5) / (40 / 5) = 4 / 8 = 0,5
La utilidad de las fracciones equivalentes reside en la posibilidad de hallar una versión más pequeña de otra, que nos vuelva menos complicado un determinado cálculo, por ejemplo. Por otro lado, reconocer dos o más fracciones equivalentes en una operación puede simplificarla si nos permite eliminarlas o asociarlas.
