Definición de ángulos adyacentes
Un ángulo es una figura geométrica que se forma con dos semirrectas que comparten un mismo vértice a modo de origen. Adyacente, por su parte, es un adjetivo que califica a lo que está ubicado al lado de algo.
Los ángulos adyacentes son aquéllos que comparten un lado y el vértice, mientras que los otros dos lados resultan semirrectas opuestas. Esta definición nos permite inferir que los ángulos adyacentes también son ángulos contiguos o consecutivos (porque cuentan con un lado en común y el mismo vértice) y ángulos suplementarios (la suma de ambos da como resultado 180°; es decir, un ángulo llano).
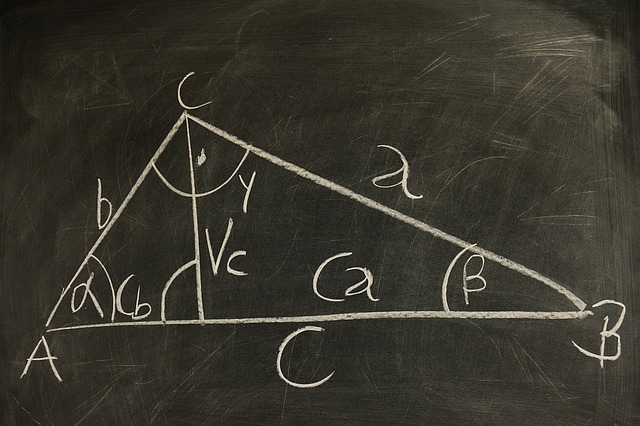
Los ángulos adyacentes comparten el vértice y un lado.
Es importante señalar que no todas las fuentes de este tema respetan el requisito de que ambos ángulos sumen un total de 180°; es decir, en muchos textos de geometría se define el concepto de ángulos adyacentes como cualquier par que tengan un lado y el vértice en común, sin necesidad de que sean suplementarios. Por esta razón, antes de consultar información al respecto, es necesario identificar la convención a la cual responde, para evitar contradicciones o falta de consistencia.
Propiedades de los ángulos adyacentes
Otras propiedades de los ángulos adyacentes es que sus cosenos tienen el mismo valor, aunque signos inversos, es decir que su valor absoluto es el mismo; por ejemplo, si tomamos dos ángulos adyacentes, uno de 120° y otro de 60°, el coseno del primero es igual al del segundo multiplicado por -1. Los senos de estos ángulos, en cambio, resultan iguales.
El coseno es un concepto perteneciente a la trigonometría, y hace referencia a la razón entre el cateto adyacente de un ángulo agudo que forme parte de un triángulo rectángulo y su hipotenusa; en otras palabras, podemos decir que el coseno del ángulo α es igual a la división de su cateto adyacente por el valor de la hipotenusa. Cabe señalar que el resultado no varía según las características del triángulo rectángulo, sino que se trata de una función del ángulo, según indica el Teorema de Tales.
Por otro lado se encuentra el seno, una función de la trigonometría que consiste en dividir el cateto opuesto a un ángulo dado por su hipotenusa.
Los ángulos adyacentes también son suplementarios y contiguos o consecutivos.
Algunos ejemplos
Si un ángulo de 44° está ubicado junto a un ángulo de 136°, con el cual comparte un lado y el vértice, podemos decir que se trata de ángulos adyacentes (44° + 136° = 180°). Esta calificación afecta a los dos ángulos, sin que impida el desarrollo de otras clasificaciones. El ángulo de 44°, además de ser adyacente del otro, es un ángulo agudo. El ángulo de 136°, por su parte, es adyacente de este ángulo agudo, pero a su vez es un ángulo obtuso.
Dos ángulos rectos (de 90° cada uno) también pueden ser ángulos adyacentes. El requisito siempre es el mismo: tienen que compartir vértice y un lado y los otros dos lados deben ser semirrectas opuestas. Si sumamos ambos ángulos rectos adyacentes, el resultado será un ángulo llano (180°).
Problemas con ángulos adyacentes
Como sucede con muchas otras clasificaciones del ámbito de las matemáticas, el concepto de ángulos adyacentes puede aplicarse a muchos problemas diferentes. Una vez que identificamos el tipo de ángulo frente al cual nos encontramos, el paso siguiente es recurrir a una fuente fiable para estudiar todas sus propiedades conocidas, y evaluar su utilidad para nuestro proyecto.
Podemos decir que no siempre los dos ángulos necesarios para dar vida a este concepto se hallan presentes de manera expresa, sino que muchas veces partimos de uno solo e imaginamos el otro para acceder a dichas propiedades, si esto nos abre las puertas a nuevas soluciones. En otras palabras, no debemos olvidar que se trata de conceptos que nacen de la observación y la teorización, con lo cual nos permiten amoldar la realidad a nuestras necesidades.
