Principio de Arquímedes: fórmula, demostración, aplicaciones
El principio de Arquímedes dice que un cuerpo sumergido total o parcialmente, recibe una fuerza vertical hacia arriba denominada empuje, la cual equivale al peso del volumen de líquido desplazado por el cuerpo.
Algunos objetos flotan en el agua, otros se hunden y algunos se sumergen parcialmente. Para hundir una pelota de playa es necesario hacer un esfuerzo, porque de inmediato se percibe esa fuerza que trata de devolverla a la superficie. En cambio una esfera de metal se hunde rápidamente.

Por otro lado, los objetos sumergidos parecen más livianos, por lo tanto existe una fuerza ejercida por el fluido que se contrapone al peso. Pero no siempre puede compensar del todo a la gravedad. Y, aunque es más evidente con el agua, los gases también son capaces de producir esta fuerza sobre los objetos inmersos en ellos.
Índice del artículo
- 1 Historia
- 2 Fórmula del principio de Arquímedes
- 3 Demostración
- 4 Aplicaciones del principio de Arquímedes
- 5 Ejemplos
- 6 Ejercicios resueltos
- 7 Referencias
Arquímedes de Siracusa (287-212 a. C.) fue a quien se debe haber descubierto este principio, siendo uno de los más grandes científicos de la historia. Cuentan que el rey Hierón II de Siracusa mandó a un orfebre fabricarle una corona nueva, para lo cual le entregó una cierta cantidad de oro.

Cuando el rey recibió la corona nueva, esta tenía el peso correcto, pero sospechó que el orfebre le había engañado agregando plata en vez de oro. ¿Cómo podía comprobarlo sin destruir la corona?
Hierón llamó a Arquímedes, cuya fama de erudito era de sobra conocida, para que le ayudara a resolver el problema. La leyenda afirma que Arquímedes estaba sumergido en la bañera cuando dio con la respuesta y, tal fue su emoción, que salió corriendo desnudo por las calles de Siracusa para buscar al rey gritando “eureka”, que significa “lo encontré”.

¿Qué encontró Arquímedes? Pues que al tomar un baño el nivel del agua en la bañera subía cuando él entraba, lo cual significa que un cuerpo sumergido desplaza un cierto volumen de líquido.
Y si sumergía la corona en agua, esta también debía desplazar un cierto volumen de agua si la corona estaba hecha de oro y otro diferente si estaba hecha de aleación con plata.

La fuerza ascensional a la que hace referencia el principio de Arquímedes es conocida como empujehidrostático o fuerza de flotación y, como hemos dicho, equivale al peso del volumen de fluido desplazado por el cuerpo al estar sumergido.
El volumen desplazado equivale al volumen del objeto que esté sumergido, ya sea total o parcialmente. Puesto que el peso de cualquier cosa es mg, y la masa del fluido es densidad x volumen, denotando como B a la magnitud del empuje, matemáticamente se tiene que:
B = mfluido x g = densidad del fluido x Volumen sumergido x gravedad
B = ρfluido x Vsumergido x g
Donde la letra griega ρ (“rho”) denota la densidad.
El peso de los objetos se calcula mediante la conocida expresión mg, sin embargo las cosas se sienten más livianas cuando están sumergidas en el agua.
El peso aparente de un objeto es el que tiene cuando está inmerso en agua u otro líquido y conociéndolo, se puede obtener el volumen de un objeto irregular como la corona del rey Hierón, como se verá a continuación.
Para ello se lo sumerge completamente en agua y sujeto de una cuerda adosada a un dinamómetro -un instrumento provisto de un resorte que sirve para medir fuerzas-. A mayor peso del objeto, mayor elongación del resorte, la cual se mide sobre una escala provista en el aparato.
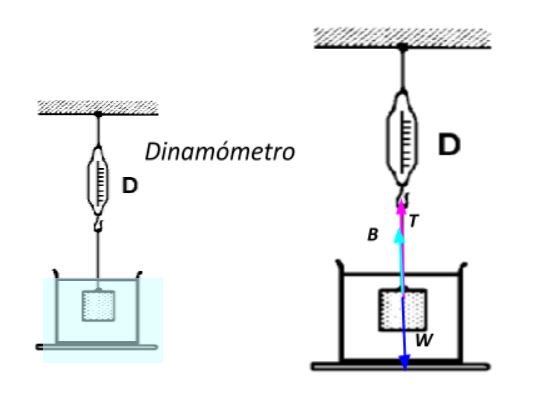
Aplicando la segunda ley de Newton sabiendo que el objeto está en reposo:
ΣFy = B + T – W = 0
El peso aparente Wa equivale a la tensión en la cuerda T:
T = Wa
Wa = mg – ρfluido . V. g
Si se requiere el volumen sumergido V, se despeja como:
V = (W – Wa) / ρfluido . g
Cuando un cuerpo se sumerge, el empuje es la fuerza resultante de todas las fuerzas que se ejercen sobre el cuerpo a través de la presión causada por el fluido que lo rodea:
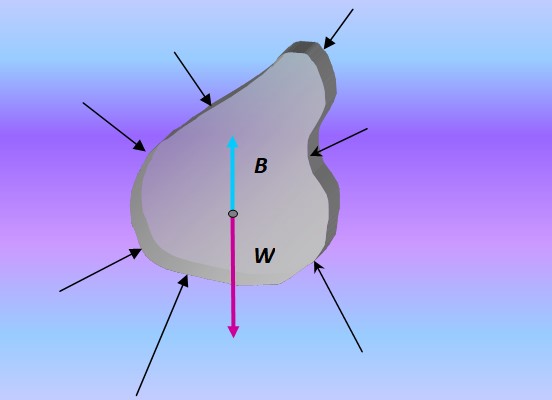
Dado que la presión aumenta con la profundidad, la resultante de estas fuerzas siempre está dirigida verticalmente hacia arriba. Por lo tanto, el principio de Arquímedes es consecuencia del teorema fundamental de la hidrostática, el cual relaciona la presión P ejercida por un fluido con la profundidad z como:
P = ρ.g.z
Para demostrar el principio de Arquímedes, se toma una pequeña porción cilíndrica de fluido en reposo para analizar las fuerzas ejercidas sobre ella, tal como se muestra en la siguiente figura. Las fuerzas sobre la superficie curva del cilindro se cancelan entre sí.
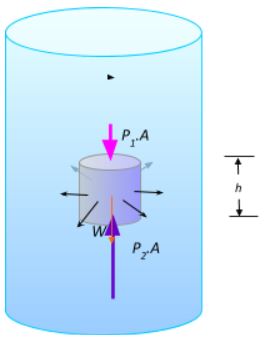
Las magnitudes de las fuerzas verticales son F1 = P1.A y F2 = P2.A, además está el peso W. Como el fluido está en equilibrio, la sumatoria de las fuerzas debe anularse:
∑Fy = P2.A- P1.A- W = 0
P2.A- P1.A= W
Ya que el empuje compensa al peso, puesto que la porción de fluido está en reposo, entonces:
B = P2.A- P1.A = W
De esta expresión se desprende que el empuje se debe a la diferencia de presiones entre la cara superior del cilindro y la inferior. Como W = mg = ρfluido. V. g, se tiene que:
B = ρfluido. Vsumergido. g
Que es precisamente la expresión para el empuje mencionada en el apartado anterior.

El principio de Arquímedes aparece en muchas aplicaciones prácticas, entre las que podemos nombrar:
– El globo aerostático. El cual por tener una densidad promedio menor que la del aire circundante, flota en él debido a la fuerza de empuje.
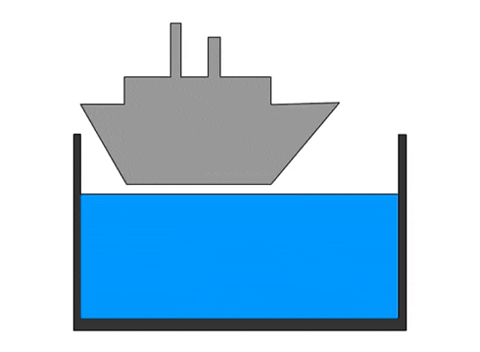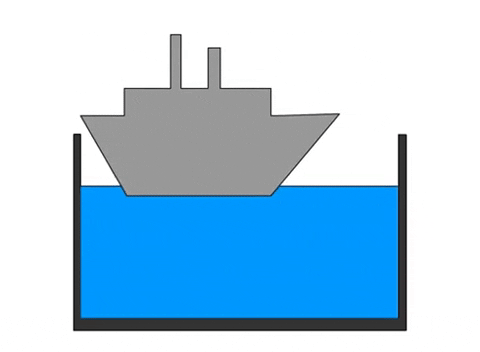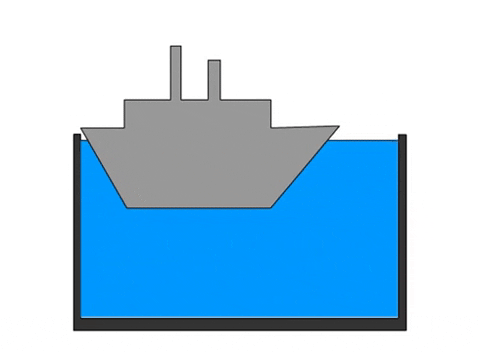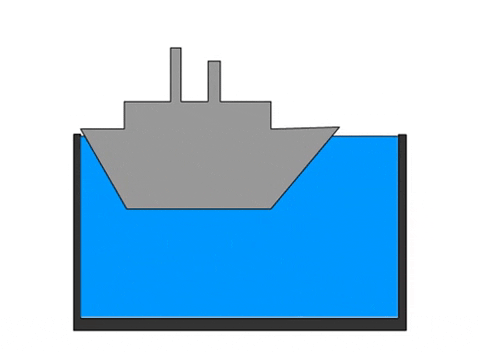
– Los barcos. El casco de los barcos es más pesado que el agua. Pero si se considera el conjunto del casco más el aire en su interior, el cociente entre la masa total y el volumen es menor que la del agua y esa es la razón por la que los barcos flotan.
– Los chalecos salvavidas. Al ser construidos de materiales livianos y porosos, son capaces de flotar porque la relación masa-volumen es menor que la del agua.
– El flotante para cerrar el grifo de llenado de un tanque de agua. Se trata de un esfera llena de aire de gran volumen que flota sobre el agua, la cual causa que la fuerza de empuje – multiplicada por el efecto palanca – cierre el tapón del grifo de llenado de un tanque de agua cuando esta ha alcanzado el nivel total.
La leyenda cuenta que el rey Hierón dio al orfebre cierta cantidad de oro para que fabricase una corona, pero el desconfiado monarca pensó que el orfebre pudo haber hecho trampa al colocar en el interior de la corona un metal menos valioso que el oro. Pero ¿cómo podía saberlo sin destruir la corona?
El rey le encargó el problema a Arquímedes y este, buscando la solución, descubrió su famoso principio.
Supongamos que la corona pesa 2,10 kg-f en el aire y 1,95 kg-f cuando está completamente sumergida en agua. En este caso, ¿hay o no hay engaño?
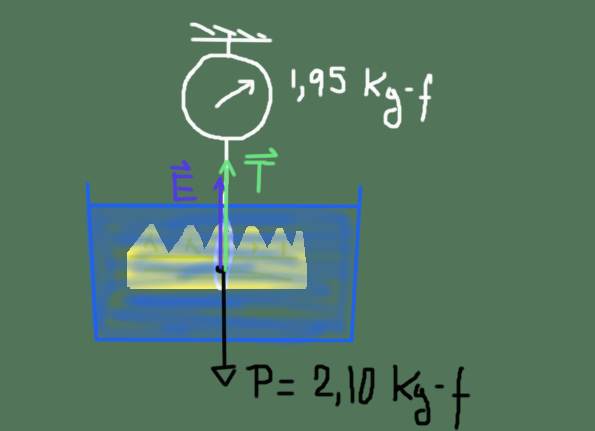
El diagrama de las fuerzas se muestra en la figura anterior. Estas fuerzas son: el pesoP de la corona, el empuje E y la tensión T de la cuerda que cuelga de la báscula.
Se conoce P = 2,10 kg-f y T = 1,95 kg-f, falta determinar la magnitud del empuje E:
T + E = P ⇒ E = P – T = (2,10 – 1,95) kg-f = 0,15 kg-f
Por otra parte, de acuerdo al principio de Arquímedes, el empuje E es equivalente al peso del agua desalojada del espacio ocupado por la corona, es decir la densidad del agua por el volumen de la corona por la aceleración de gravedad:
E = ρagua⋅V⋅g = 1000 kg/m^3 ⋅ V ⋅ 9,8m/s^2 = 0,15 kg ⋅ 9,8 m/s^2
De donde puede calcularse el volumen de la corona:
V = 0,15 kg / 1000 kg/m^3 = 0,00015 m^3
La densidad de la corona es el cociente entre la masa de la corona fuera del agua y el volumen de la misma:
Densidad de la corona = 2,10 kg / 0,00015 m^3 = 14000 kg/m^3
La densidad del oro puro se puede determinar por un procedimiento similar y el resultado es de 19300 kg/m^3.
Comparando las dos densidades es evidente que la corona ¡no es de oro puro!
Basándose en los datos y el resultado del ejemplo 1, es posible determinar cuánto oro fue robado por el orfebre en el caso que parte del oro haya sido sustituido por plata, la cual tiene una densidad de 10500 kg/m^3.
Llamaremos ρc a la densidad de la corona, ρo a la densidad del oro y ρp a la densidad de la plata.
La masa total de la corona es:
M = ρc⋅V = ρo⋅Vo + ρp⋅Vp
El volumen total de la corona es el volumen de plata más el volumen de oro:
V = Vo + Vp ⇒ Vp = V – Vo
Sustituyendo en la ecuación de la masa queda:
ρc⋅V = ρo⋅Vo + ρp⋅(V – Vo) ⇒ (ρo – ρp)Vo = (ρc – ρp)V
Es decir que el volumen de oro Vo que contiene la corona de volumen total V es:
Vo = V⋅(ρc – ρp)/(ρo – ρp) = …
…= 0,00015 m^3 (14000 – 10500)/(19300 – 10500) = 0,00005966 m^3
Para saber el peso en oro que contiene la corona multiplicamos Vo por la densidad del oro:
Mo = 19300 * 0,00005966 = 1,1514 kg
Como la masa de la corona es 2,10 kg, sabemos que 0,94858 kg de oro fueron robados por el orfebre y sustituidos por plata.
Un enorme globo de helio es capaz de sostener en equilibrio (sin subir ni descender) a una persona.
Suponga que el peso de la persona, más la canasta, cuerdas y globo es de 70 kg. ¿Cuál es el volumen de helio necesario para que esto ocurra? ¿Qué tamaño ha de tener el globo?
Solución
Supondremos que el empuje es producido principalmente por el volumen de helio y que el empuje del resto de los componentes es muy pequeño en comparación con el del helio que ocupa mucho más volumen.
En este caso, se requerirá de un volumen de helio capaz de proporcionar un empuje de 70 kg + el peso del helio.
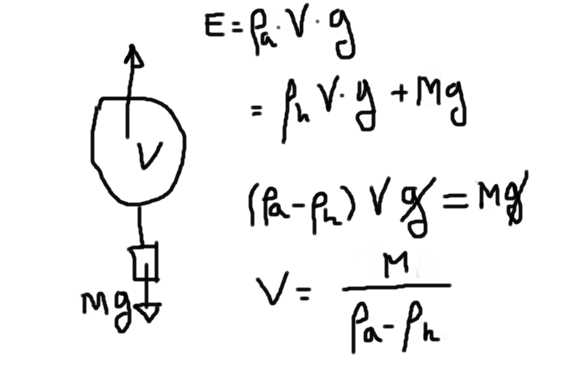
El empuje es el producto del volumen de helio por la densidad del helio por la aceleración de gravedad. Ese empuje debe compensar el peso del helio más el peso de todo el resto.
Da⋅V⋅g = Da⋅V⋅g + M⋅g
de donde se concluye que V = M / (Da – Dh)
V = 70 kg / (1.25 – 0,18)kg/m^3 = 65.4 m^3
Es decir, se requieren de 65.4 m^3 de helio a presión atmosférica para que haya sustentación.
Si suponemos un globo esférico podemos encontrar el radio del mismo a partir de la relación entre el volumen y el radio de una esfera:
V = (4/3)⋅π⋅R^3
De donde R = 2,49 m. Es decir se requerirá de un globo de 5 m de diámetro lleno de helio.
Los materiales de menor densidad que el agua flotan en la misma. Suponga que tiene cubos de poliestireno (corcho blanco), madera y hielo. Sus densidades en kg por metro cúbico son respectivamente: 20, 450 y 915.
Encuentre qué fracción del volumen total queda fuera del agua y que altura sobresale respecto a la superficie del agua tomando como densidad de esta última 1000 kilogramos por metro cúbico.
Solución
La flotabilidad se da cuando el peso del cuerpo es igual al empuje debido al agua:
E = M⋅g
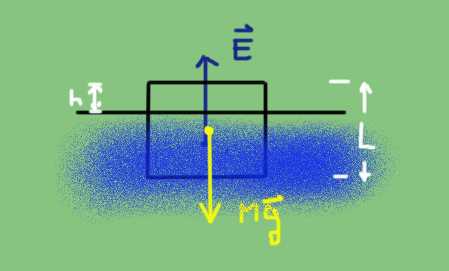
El peso es la densidad de cuerpo Dc multiplicada por su volumen V y por la aceleración de gravedad g.
El empuje es el peso del fluido desplazado según el principio de Arquímedes y se calcula multiplicando la densidad D del agua por el volumen sumergido V’ y por la aceleración de gravedad.
Es decir que:
D⋅V’⋅g = Dc⋅V⋅g
Lo que significa que la fracción de volumen sumergido es igual al cociente entre la densidad del cuerpo y la densidad del agua.
(V’/V) = (Dc/D)
Es decir que la fracción de volumen sobresaliente (V’’/V) es
(V’’/V) = 1 – (Dc/D)
Si h es la altura sobresaliente y L el lado del cubo la fracción de volumen puede escribirse como
(h⋅L^2)/(L^3) = h/L, es decir que la fracción de altura sobresaliente es también
(h/L) = 1 – (Dc/D)
Entonces los resultados para los materiales pedidos son:
Poliestireno (corcho blanco):
(h/L) =(V’’/V) = 1 – (Dc/D)= 1- (20/1000) = 98% fuera del agua
Madera:
(h/L) =(V’’/V) = 1 – (Dc/D)= 1- (450/1000) = 55% fuera del agua
Hielo:
(h/L) =(V’’/V) = 1 – (Dc/D)= 1- (915/1000) = 8.5% fuera del agua
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill. 417-455.
- Cengel Y, Cimbala J. 2011.Mecánica de Fluidos. Fundamentos y aplicaciones. Primera edición. McGraw Hill.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 4. Fluidos y Termodinámica. Editado por Douglas Figueroa (USB). 1 – 42.
- Giles, R. 2010. Mecánica de los fluidos e hidraulica. McGraw Hill.
- Rex, A. 2011. Fundamentos de Física. Pearson. 239-263.
- Tippens, P. 2011. Física: Conceptos y Aplicaciones. 7ma Edición. McGraw Hill.
