Ciclo Brayton: proceso, eficiencia, aplicaciones, ejercicios
El ciclo Brayton es un ciclo termodinámico que consta de cuatro procesos y se aplica a un fluido termodinámico compresible como un gas. Su primera mención data de finales del siglo XVIII, si bien pasó algún tiempo antes de que fuera planteado por primera por James Joule. Por eso también se le conoce como el ciclo Joule.
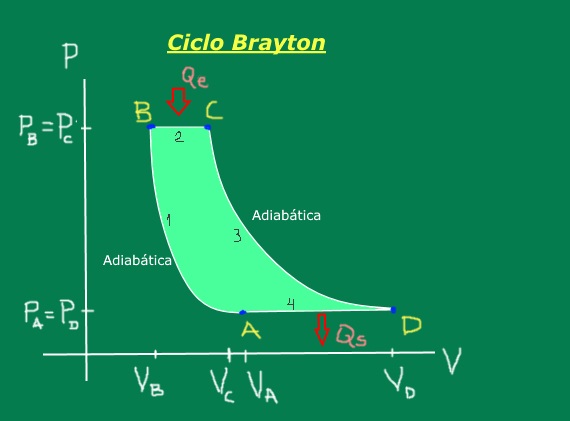
Consta de las siguientes etapas, que se ilustran convenientemente en el diagrama presión – volumen de la figura 1: compresión adiabática (no se intercambia calor), expansión isobárica (ocurre a presión constante), expansión adiabática (no se intercambia calor) y compresión isobárica (ocurre a presión constante).
Índice del artículo
- 1 Proceso y descripción
- 2 Eficiencia en función de la temperatura, calor y presión
- 3 Aplicaciones
- 4 Ejercicios resueltos
- 5 Referencias
El ciclo Brayton es el ciclo termodinámico ideal que mejor se aplica para explicar el funcionamiento termodinámico de las turbinas a gas y mezcla aire-combustible, empleadas para la generación de energía eléctrica y en los motores de aviación.
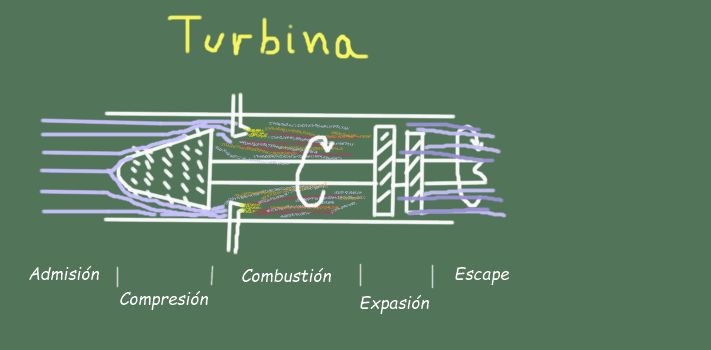
Por ejemplo, en el funcionamiento de una turbina hay varias etapas en el flujo de gas de operación, que veremos a continuación.
Consiste en la entrada de aire a temperatura y presión ambiental por la apertura de entrada de la turbina.
El aire es comprimido mediante unas paletas giratorias contra otras fijas en la sección del compresor de la turbina. Esta compresión es tan rápida que prácticamente no hay intercambio de calor, por lo que se modela mediante el proceso adiabático AB del ciclo Brayton. El aire a la salida del compresor ha elevado su presión y temperatura.
El aire se mezcla con gas propano o combustible pulverizado que se introduce por los inyectores de la cámara de combustión. La mezcla produce una reacción química de combustión.
Esta reacción es la que aporta el calor que hace aumentar la temperatura y la energía cinética de las partículas del gas que se expande en la cámara de combustión a presión constante. En el ciclo Brayton este paso se modela con el proceso BC que ocurre a presión constante.
En la sección de la turbina propiamente dicha, el aire continúa expandiéndose contra las paletas de la turbina haciéndola rotar y produciendo trabajo mecánico. En este paso el aire baja su temperatura pero sin intercambiar calor prácticamente con el entorno.
En el ciclo de Brayton este paso se simula como un proceso de expansión adiabática CD. Parte del trabajo de la turbina se transfiere al compresor y la otra se usa para mover un generador o una hélice.
El aire saliente está a presión constante igual a la ambiental y cede calor a la enorme masa de aire externo, por lo que en poco tiempo toma la misma temperatura del aire de entrada. En el ciclo Brayton este paso se simula con el proceso a presión constante DA, cerrando el ciclo termodinámico.
Nos proponemos calcular la eficiencia del ciclo Brayton, para lo cual partimos de la definición de la misma.
En una máquina térmica la eficiencia se define como el trabajo neto realizado por la máquina dividido entre la energía calorífica aportada.
El primer principio de la termodinámica establece que el calor neto aportado a un gas en un proceso termodinámico es igual a la variación de la energía interna del gas más el trabajo realizado por el mismo.
Pero en un ciclo completo la variación de la energía interna es nula, por lo que se tiene que el calor neto aportado en el ciclo es igual al trabajo neto realizado.
La expresión anterior nos permite escribir la eficiencia en función del calor absorbido o entrante Qe (positvo) y el calor cedido o saliente Qs (negativo).
En el ciclo Brayton el calor entra en el proceso isobárico BC y sale en el proceso isobárico DA.
Suponiendo que a n moles de gas a presión constante que se le suministra calor sensible Qe en el proceso BC, entonces su temperatura se incrementa de Tb a Tc según la siguiente relación:
El calor saliente Qs puede calcularse en forma similar mediante la siguiente relación que se aplica al proceso a presión constante DA:
Sustituyendo estas expresiones en la expresión que nos da la eficiencia en función del calor entrante y calor saliente, haciendo las simplificaciones pertinentes se obtiene la siguiente relación para la eficiencia:
Es posible simplificar el resultado anterior si tomamos en cuenta que Pa = Pd y que Pb = Pc dado que los procesos AD y BC son isobáricos, es decir a la misma presión.
Además, como los procesos AB y CD son adiabáticos se cumple la relación de Poisson para ambos procesos:
Donde gamma representa el cociente adiabático, es decir, el cociente entre la capacidad calorífica a presión constante y la capacidad calorífica a volumen constante.
Usando estas relaciones y la relación de la ecuación de estado de un gas ideal podemos obtener una expresión alternativa para relación de Poisson:
Como sabemos que Pa = Pd y que Pb = Pc sustituyendo y dividiendo miembro a miembro se obtiene la siguiente relación entre temperaturas:
Si a cada miembro de la ecuación anterior se le resta la unidad, se resuelve la diferencia y se arreglan los términos puede demostrarse que:
La expresión obtenida para la eficiencia del ciclo Brayton en función de las temperaturas puede reescribirse para ser formulada en función del cociente de la presión a la salida y entrada del compresor.
Esto se logra si se sabe la relación de Poisson entre los puntos A y B en función de la presión y la temperatura, obteniéndose que la eficiencia del ciclo se expresa así:
Una relación típica de cociente de presiones es 8. En este caso el ciclo de Brayton tiene un rendimiento teórico de 45%.
El ciclo Brayton como modelo se aplica a las turbinas de gas que se usan en las plantas termoeléctricas con el fin de mover los generadores que producen la electricidad.
También es un modelo teórico que se ajusta bien al funcionamiento de los motores turbohélice que se usan en los aviones, pero no es aplicable en absoluto en los turborreactores de los aviones.
Cuando interesa maximizar el trabajo producido por la turbina para mover los generadores o las hélices de un avión, entonces es cuando se aplica el ciclo Brayton.

En los turborreactores de los aviones, en cambio, no interesa convertir la energía cinética de los gases en combustión para producir trabajo, que sería apenas el necesario para realimentar el turbocompresor.
Al contrario, interesa obtener la mayor energía cinética posible del gas expulsado, para que de acuerdo al principio de acción y reacción, se obtenga el impulso de la aeronave.
Una turbina a gas de las que se usan en las centrales termoeléctricas tiene una presión a la salida del compresor de 800 kPa. La temperatura del gas entrante es la ambiental y es de 25 Celsius, y la presión es de 100 kPa.
En la cámara de combustión la temperatura se eleva hasta 1027 Celsius para ingresar a la turbina.
Determine la eficiencia del ciclo, la temperatura del gas a la salida del compresor y la temperatura del gas a la salida de la turbina.
Solución
Como tenemos la presión del gas a la salida del compresor y sabemos que la presión de entrada el la presión atmosférica, entonces es posible obtener el cociente de presiones:
r = Pb/Pa = 800 kPa / 100 KPa = 8
Como el gas con el que opera la turbina es una mezcla de aire y gas propano, se aplica entonces el coeficiente adiabático para un gas ideal diatómico, es decir, un gamma de 1,4.
La eficiencia entonces se calcularía así:
Donde hemos aplicado la relación que da la eficiencia del ciclo Brayton en función del cociente de presiones en el compresor.
Cálculo de la temperatura
Para determinar la temperatura a la salida del compresor, o lo que es lo mismo la temperatura con la que ingresa el gas en la cámara de combustión, aplicamos la relación de la eficiencia con las temperaturas de entrada y salida del compresor.
Si de esa expresión despejamos la temperatura Tb obtenemos:
Como dato del ejercicio tenemos que después de la combustión la temperatura se eleva hasta 1027 Celsius, para ingresar a la turbina. Parte de la energía térmica del gas se emplea para mover la turbina, por lo que la temperatura a la salida de la misma ha de ser menor.
Para calcular la temperatura a la salida de la turbina emplearemos una relación entre temperatura obtenida anteriormente:
De allí despejamos Td para obtener la temperatura a la salida de la turbina. Después de realizar los cálculos la temperatura que se obtiene es:
Td = 143,05 Celsius.
Una turbina a gas sigue el ciclo Brayton. La relación de presiones entre las salida y entrada del compresor es 12.
Suponga la temperatura ambiente de 300 K. Como dato adicional se conoce que la temperatura del gas después de la combustión (previo a la entrada a la turbina) es de 1000K.
Determine la temperatura a la salida del compresor, y la temperatura a la salida de la turbina. Determine también cuántos kilogramos de gas circulan por la turbina en cada segundo, sabiendo que la potencia de la misma es de 30 KW.
Suponga el calor específico del gas como constante y tome el valor del mismo a temperatura ambiente: Cp = 1,0035 J / (kg K).
Suponga también que la eficiencia de compresión en el compresor y de descompresión en la turbina es del 100%, lo cual es una idealización porque en la práctica siempre ocurren pérdidas.
Solución
Para determinar la temperatura a la salida del compresor, conocida la temperatura a la entrada, debemos recordar que se trata de una compresión adiabática, por lo que puede aplicarse la relación de Poisson para el proceso AB.
Para cualquier ciclo termodinámico, el trabajo neto siempre será igual al calor neto intercambiado en el ciclo.
El trabajo neto por ciclo de operación puede expresarse entonces en función de la masa de gas que circuló en ese ciclo y las temperaturas.
En esta expresión m es la masa de gas que circuló por la turbina en un ciclo de operación y Cp el calor específico.
Si tomamos la derivada respecto al tiempo de la expresión anterior obtenemos la potencia media neta en función del caudal másico.
Despejando m punto, y sustituyendo las temperaturas, la potencia y la capacidad calorífica del gas obtenemos un flujo másico de 1578,4 kg/s.
- Alfaro, J. Ciclos Termodinámicos. Recuperado de: fis.puc.cl.
- Fernández J.F. Ciclo Brayton. Turbina a gas. U.T.N. (Mendoza). Recuperado de: edutecne.utn.edu.ar.
- Universidad de Sevilla. Departamento de Física. Ciclo Brayton. Recuperado de: laplace.us.es.
- Universidad Nacional Experimental del Táchira. Fenómenos de Transporte. Ciclos de potencia por gas. Recuperado de: unet.edu.ve.
- Wikipedia. Ciclo Brayton. Recuperado de: wikiwand.com
- Wikipedia. Turbina de gas. Recuperado de: wikiwand.com.
