Segunda condición de equilibrio: explicación, ejemplos, ejercicios
La segunda condición de equilibrio establece que la sumatoria de los torques o momentos producidos por todas las fuerzas que actúan sobre un cuerpo, sin importar respecto a qué punto se calculan, debe anularse para que dicho cuerpo se encuentre en equilibrio estático o dinámico.
Denotando al torque o momento de la fuerza mediante la letra griega τ, matemáticamente se expresa así:
∑ τ = 0

La letra negrita indica la naturaleza vectorial del momento, el cual debe anularse respecto a cualquier punto que se escoja como centro de giro. De esta manera, anulando el torque neto se garantiza que el objeto no comience a girar o se vuelque.
Sin embargo, si el objeto ya se encontraba girando previamente, y el torque neto desaparece de súbito, la rotación continuará, pero con rapidez angular constante.
La segunda condición de equilibrio se usa en conjunto con la primera condición, la cual dice que la sumatoria de las fuerzas sobre un cuerpo debe ser nula, a fin de que no se traslade, o que si lo hace, sea con movimiento rectilíneo uniforme:
∑ F = 0
Ambas condiciones se aplican a los cuerpos extendidos, aquellos cuyas dimensiones son mensurables. Cuando se supone que un objeto es una partícula, no tiene sentido hablar de rotaciones, y basta con la primera condición para garantizar el equilibrio.
Ejemplos
La segunda condición de equilibrio se pone de manifiesto en un sinnúmero de situaciones:
Al subir por la escalera
Al apoyar una escalera sobre el piso y la pared, necesitamos suficiente roce, sobre todo en el piso, como para garantizar que la escalera no resbale. Si intentamos trepar sobre una escalera apoyada en un piso aceitoso, mojado o resbaladizo, no es difícil anticipar que nos caeremos.
Para poder usar con confianza la escalera, es necesario que esta se encuentre en equilibrio estático mientras se sube y cuando se está en el peldaño que se necesita.
Trasladando un armario
Cuando se desea trasladar un mueble alto como un armario, o cualquier pieza cuyo alto sea mayor que su ancho, es conveniente empujar sobre un punto bajo, para evitar el volcamiento, de esta forma es más probable que el mueble se deslice en vez de girar y tumbarse.
En tales circunstancias el mueble no necesariamente está en equilibrio, pues podría trasladarse aceleradamente, pero al menos no volcaría.
Balcones
Los balcones que sobresalen de los edificios deben construirse garantizando que, aunque haya muchas personas encima, no se vuelque y colapse.
Dieléctricos en campos eléctricos externos
Al colocar un material dieléctrico en un campo eléctrico externo, las moléculas se mueven y rotan hasta adoptar una posición de equilibrio, creando un campo eléctrico en el interior del material.
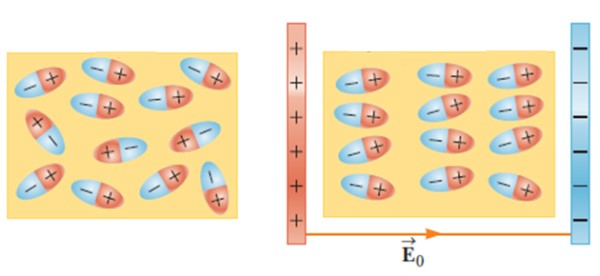
Este efecto hace que la capacidad de un condensador aumente cuando se introduce entre sus armaduras un material como vidrio, goma, papel o aceite.
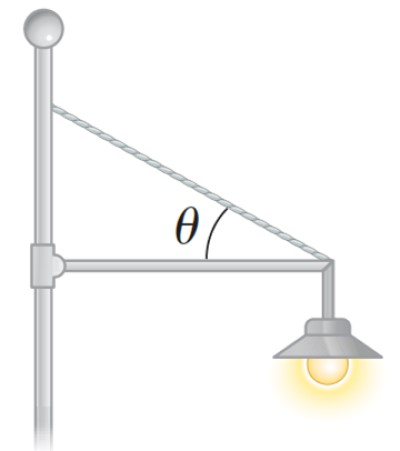
Letreros y lámparas
Es común que muchos locales cuelguen avisos en la pared del edificio, para que sean visibles a los transeúntes.
El cartel se sujeta mediante una barra y un cable, ambos fijos en la pared mediante soportes. Las diversas fuerzas que actúan deben asegurar que el cartel no se caiga, para lo cual entran en acción las dos condiciones de equilibrio.
También se puede colocar de esta manera un reflector en un parque, como en la siguiente figura:
¿Cómo calcular el torque neto o momento neto de una fuerza?
El torque o momento de una fuerza, denotado mediante τ o M en algunos textos, se calcula siempre respecto a algún punto por donde pasa el eje de rotación.
Se define como el producto vectorial entre el vector de posición r, que va dirigido desde dicho eje hasta el punto de aplicación de la fuerza y la fuerza F:
τ = r × F
Siendo un vector, es necesario expresar el torque dando su magnitud, dirección y sentido. La magnitud viene dada por:
τ = rF.sen θ
Regla de la mano derecha para el producto vectorial
Cuando el problema está en el plano, la dirección del torque es perpendicular al papel o a la pantalla y el sentido viene determinado por la regla de la mano derecha, en la que el índice apunta hacia r, el dedo medio hacia F y el pulgar señala hacia dentro o hacia fuera del papel.
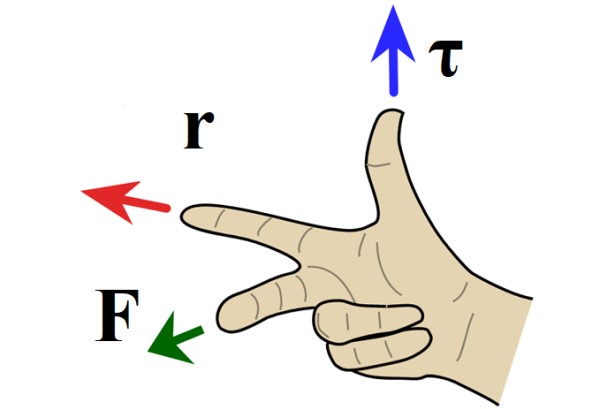
Cuando el torque apunta hacia afuera del papel la rotación es en sentido contrario a las agujas del reloj y se le asigna signo positivo por convención. Si en cambio el torque se dirige hacia dentro de la hoja, la rotación es en sentido de las manecillas y de signo negativo.
Para encontrar el torque neto se escoge un punto conveniente para el cálculo, que puede ser aquel en el cual actúe la mayor cantidad de fuerzas. En este caso el momento de estas fuerzas es nulo, por tener un vector posición r de magnitud 0.
Se puede elegir cualquier punto que ofrezca la información suficiente para despejar la incógnita que pida el problema a resolver. Vamos a verlo con más detalle seguidamente.
Ejercicio resuelto
El reflector de la figura siguiente tiene 20 kg de masa y se sostiene mediante una barra delgada horizontal, de masa despreciable y longitud L, que está articulada a un poste. El cable, también liviano, que ayuda a sostener al reflector forma un ángulo θ = 30 º con la barra. Calcular:
a) La tensión en el cable
b) La magnitud de la fuerza F que el poste ejerce sobre la barra a través de la bisagra.
Solución
Aplicaremos la primera condición de equilibrio ∑ F = 0 a las fuerzas mostradas en el diagrama:
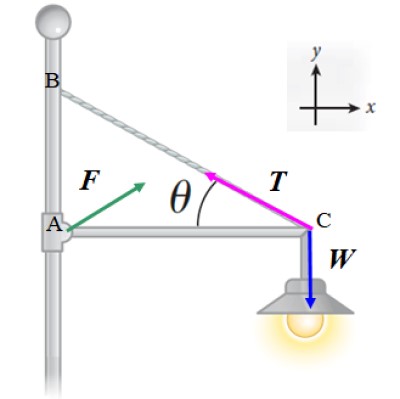
F + T + W = 0
Nótese que la magnitud y la dirección de F están por determinarse aún, pero suponemos que tiene dos componentes: Fx y Fy. De esta manera obtenemos dos ecuaciones:
Fx –T. cos θ = 0
Fy – W + T⋅ sen θ = 0
Ahora apliquemos la segunda condición de equilibrio, eligiendo el punto A, ya que no conocemos la magnitud de F ni la de T. Al escoger este punto, el vector rA es nulo, por lo tanto el momento de F es nulo y la magnitud de F no aparecerá en la ecuación:
-W⋅L + T⋅sen θ⋅L = 0
Por lo tanto:
T.sen θ.L = W.L
T = W/sen θ = (20 kg x 9.8 m/s2) / sen 30 º = 392 N
Conociendo la magnitud de T podemos despejar la componente Fx:
Fx = T⋅ cos θ = 392 cos 30º N = 339. 5 N
Y seguidamente componente Fy:
Fy = W – T⋅ sen θ = (20 kg x 9.8 m/s2) – 392⋅sen 30 º = 0
Luego, podemos expresar F así:
F = 339.5 N x
Se trata pues, de una fuerza horizontal. Esto se debe a que consideramos que la barra tenía peso despreciable.
Si se hubiese escogido el punto C para hacer el cálculo del momento resultante, los vectores rT y rW son nulos, por lo tanto:
M = Fy⋅L = 0
Se concluye que Fy = 0. De esta forma:
– W + T⋅ sen θ = 0
T = W/ sen θ
Que es el mismo resultado obtenido inicialmente al escoger el punto A como el sitio donde pasa el eje de rotación.
Temas de interés
Primera condición de equilibrio.
Referencias
- Bedford, 2000. A. Mecánica para Ingeniería: Estática. Addison Wesley.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 4. Sistemas de Partículas. Editado por Douglas Figueroa (USB).
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
