Serie de Fibonacci: propiedades, relaciones naturales, aplicaciones
La serie o sucesión de Fibonacci es una secuencia de números que se obtiene comenzando con el 0 y el 1, prosigue con la suma de ellos: 0 +1=1, a continuación la suma de los dos anteriores: 1 + 1 = 2 y así sucesivamente.
Siguiendo este procedimiento se obtienen los demás términos, veamos: 2 + 1 = 3, 3 + 2 = 5, 5 + 3 = 8, 8 +5 = 13…

El procedimiento se repite tantas veces como se quiera. De esta forma, la sucesión de Fibonacci adquiere la forma: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55… Los números que la conforman se llaman números de Fibonacci.
Índice del artículo
- 1 Historia
- 2 El problema de los conejos de Fibonacci
- 3 Propiedades de la serie de Fibonacci
- 4 Aplicaciones
- 5 Referencias
La sucesión de Fibonacci recibe su nombre de un matemático italiano que vivió en la edad media: Leonardo de Pisa, también conocido como Fibonacci (1175-1250).

Leonardo pasó la infancia en el norte de África y viajó por todo el Mediterráneo, donde conoció el sistema de numeración indo arábigo y quedó encantado con él. Probablemente los maestros árabes de Leonardo le enseñaron acerca de la sucesión, que era ya conocida por los matemáticos hindúes.
Posteriormente, al regresar a Pisa Fibonacci escribió un libro llamado Liber Abaci (el Libro del Ábaco), donde además de destacar las ventajas de los números indo arábigos frente a la numeración romana e introducir el 0, planteó un problema acerca de la reproducción de los conejos.
Y la solución a este problema la constituyen precisamente los números de la sucesión de Fibonacci.
Leonardo de Pisa no se adjudicó la creación de la sucesión; solamente la mencionó en su libro como una curiosidad, que llamó la atención de muchos estudiosos que le siguieron. Entre estos estaba el matemático francés del siglo XIX Edouard Lucas, quien al estudiar la sucesión la bautizó con el nombre del sabio medieval que la dio a conocer en occidente.
El problema dice así: se tiene una pareja de conejos que viven por siempre, que a los dos meses es fértil. Una vez lograda la madurez, tienen una pareja de conejos bebés de diferente sexo cada mes, que también tardan dos meses en reproducirse y pasan a tener una pareja de conejos mensual.
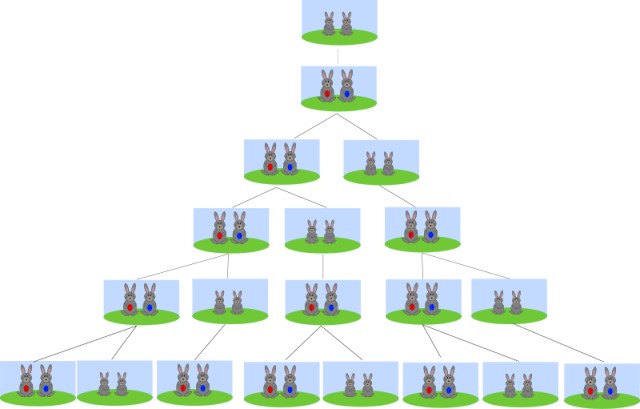
Empezando con un par de conejos recién nacidos, ¿cuántos pares de conejos habrá en un mes? ¿Cuántos pares de conejos habrá al cabo de 2, 3 y 4 meses? ¿Y cuántos habrá al cabo de 6 meses?
La respuesta está en los números de Fibonacci. Al cabo de 1 mes hay 1 par de conejos, la pareja original, pues solamente se reproducen al cabo de 2 meses.
Luego de 2 meses hay 2 parejas de conejos: la pareja original y su primera camada.
A los 3 meses, tendremos 3 parejas, incluyendo la pareja original, su primera camada y una nueva.
Al llegar al 4to mes, tendremos a la pareja original, la primera camada que a su vez tiene a sus primeros hijos, la camada del tercer mes y una nueva camada. En total 5 parejas de conejos.
Pero estos son los números de la secuencia de Fibonacci, por lo tanto al cabo de 6 meses habrá 13 parejas de conejos, ya que cada mes se suman las parejas de los dos meses anteriores.
A continuación citamos algunas propiedades interesantes de la sucesión de Fibonacci.
La fórmula recursiva para hallar los términos de la sucesión es:
an+1 = an + an-1 para n mayor o igual a 2.
Donde n = 2, 3, 4, … Es decir, para encontrar el séptimo término a7, hacemos n=6, de manera que 6+1=7. Necesitamos conocer los términos a5 y a6, de la lista que aparece en la introducción a5 = 5 y a6 = 8, por lo tanto a7 = 5+8 = 13.
Si no se conocen los dos términos anteriores al que queremos hallar, entonces podemos usar la siguiente fórmula:
Los números an y an+1 son coprimos, es decir, son primos entre sí, lo cual significa que no tienen factores primos en común.
Una propiedad muy interesante es la del cociente entre los términos a2n y an, el cual vale 1, cuando n=1. Es decir:
a2 / a1 = 1
Lo podemos comprobar fácilmente con la lista de números de Fibonacci.
Por otro lado, si n ≠ 1, entonces el cociente es:
a2n / an = an + 2an-1
Por ejemplo si n= 3, entonces a 2n = a6 = 8 y a3 = 2. Pues bien:
8/2 = 2 + 2. a2 = 2 + 2. 1
En efecto: 8/2 = 4 y 2 + (2.1) = 4. Se puede verificar que se cumple con cualquier valor de n.
El cociente rn = an+1 / an , cuando n se hace grande, converge a la razón de oro o proporción áurea, un número irracional que surge con frecuencia en la naturaleza, dado por:

Las ramas de ciertos árboles van saliendo cada año conforme a la sucesión de Fibonacci. El primer año el tronco crece sin echar ninguna rama, al cabo de un año produce una y así durante cada año. A su vez cada rama puede echar otra nueva al cabo de uno año, igual que se reproducen los conejos.
El centro de las flores de girasol contiene las semillas dispuestas en haces de espirales logarítmicas, en uno y otro sentido, cuyas cantidades corresponden a dos números de Fibonacci consecutivos.
Los números de Fibonacci están presentes en la cantidad de pétalos de las flores de girasol y margarita, así como en numerosos patrones en los cuales las plantas disponen sus hojas.
Los expertos aseguran que de esta forma las plantas optimizan el espacio para que hojas y flores tengan un crecimiento óptimo.
Con un punto central como lugar de partida, estas estructuras crecen y reciben luz solar, por lo tanto las nuevas hojas y pétalos deben tapar lo menos posible a las que salieron primero. Y la mejor manera de lograrlo es adoptando un patrón de crecimiento en términos de la secuencia de Fibonacci.
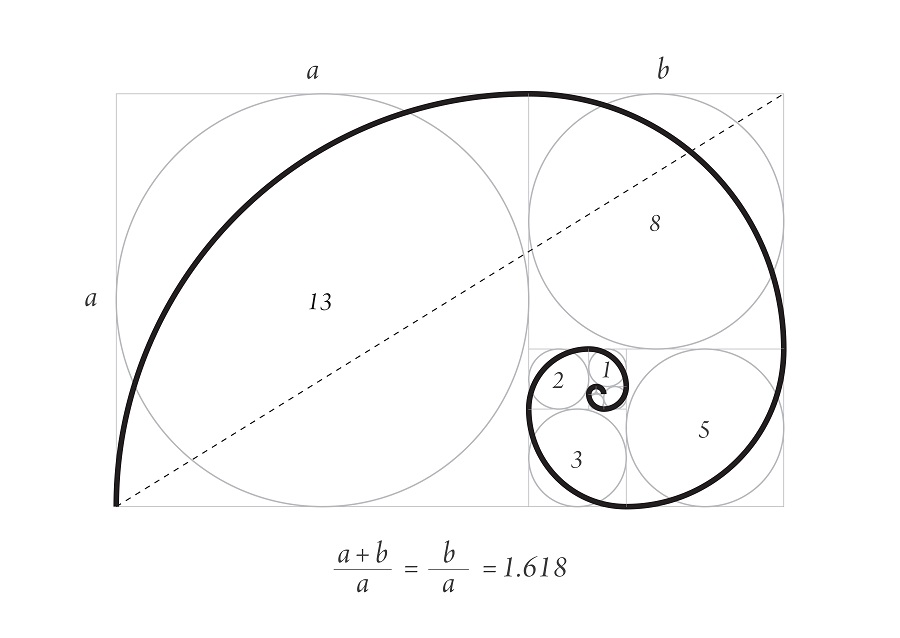
La espiral de Durero de la imagen superior forma parte del patrón de crecimiento de las conchas en animales marinos y los cuernos de algunos rumiantes.
Comienza con dos cuadrados de lado 1, uno encima del otro, luego un cuadrado de lado 2 al lado, lo que conforma un rectángulo de lado 3, cuyos lados tienen la proporción áurea.
Debajo se construye un cuadrado de lado 3 y a la izquierda un cuadrado de lado 5. Encima hay un cuadrado de lado 8 y a la derecha un cuadrado de lado 13. Estos son los primeros números de la sucesión.
Por último se traza la espiral tocando los puntos de las esquinas de los cuadrados, como se ve en la figura.
La sucesión de Fibonacci se aplica en diversos campos:
-En el arte la proporción áurea relacionada con la sucesión de Fibonacci aparece en personas y cosas representadas por grandes artistas como Leonardo da Vinci, Miguel Ángel y Alberto Durero.
-Las proporciones del Partenón en Atenas también responden al número de oro.
-En las composiciones de Mozart, Beethoven, Schubert y Debussy.
-Para diseñar objetos cuyas proporciones luzcan armoniosas a los ojos humanos, como tarjetas de crédito, envases, banderas.
-En el mercado de valores se usa para predecir qué los precios revierte su tendencia.
- Sucesión de Fibonacci. Recuperado de: blogeducastur.es.
- Stewart, J. 2007. Precálculo. 5ta. Edición. Cengage Learning.
- Vargas, M. Aplicaciones de la sucesión de Fibonacci. Recuperado de: matesup.cl.
- Wikipedia. Fibonacci number. Recuperado de: en.wikipedia.org.
