Ley de los gases ideales: fórmula y unidades, aplicaciones, ejemplos
La ley de los gases ideales es una ecuación de estado que describe una relación entre las funciones de estado asociadas con el gas ideal; tales como la temperatura, la presión, el volumen y el número de moles. Esta ley permite estudiar sistemas gaseosos reales comparándolos con sus versiones idealizadas.
Un gas ideal es un gas teórico, compuesto por partículas puntuales o esféricas que se mueven al azar; con gran energía cinética, donde la única interacción entre ellas son los choques completamente elásticos. Además, cumplen con la ley del gas ideal.

A presión y temperatura estándar (STP): 1 atm de presión, y una temperatura de 0 ºC, la mayoría de los gases reales se comportan cualitativamente como gases ideales; siempre que sus densidades sean bajas. Las grandes distancias intermoleculares o interatómicas (para gases nobles) facilitan tales aproximaciones.
Bajo condiciones STP el oxígeno, el nitrógeno, el hidrógeno, los gases nobles y algunos gases en forma de compuesto, como el dióxido de carbono, se comportan como un gas ideal.
El modelo de gas ideal tiende a fallar a temperaturas bajas, presiones altas, y a densidades de partículas altas; cuando las interacciones intermoleculares, así como el tamaño de las partículas, se vuelven importantes.
La ley de los gases ideales es una composición de tres leyes de los gases: la ley de Boyle y Mariotte, la ley de Charles y Gay-Lussac, y la ley de Avogadro.
Índice del artículo
- 1 Fórmula y unidades
- 2 ¿Qué establece la ley de los gases ideales?
- 3 Aplicaciones
- 4 Ejemplos de cálculos
- 5 Referencias

La ley de los gases se expresa matemáticamente con la fórmula:
PV =nRT
Donde P es la presión ejercida por un gas. Usualmente viene expresada con la unidad de atmósfera (atm), aunque puede expresarse en otras unidades: mmHg, pascal, bar, etc.
El volumen V ocupado por un gas suele expresarse con unidad del litro (L). Mientras n es el número de moles, R la constante universal de los gases, y T la temperatura expresada en Kelvin (K).
La expresión más usada en los gases para R equivale a 0,08206 L·atm·K-1·mol-1. Aunque la unidad SI para la constante de los gases tiene un valor de 8,3145 J·mol-1·K-1. Ambas son válidas siempre y cuando se tenga cuidado con las unidades de las otras variables (P, T y V).
La ley de los gases ideales es una combinación de la ley de Boyle-Mariotte, la ley de Charles-Gay-Lussac y la ley de Avogadro.
Ley de Boyle-Mariotte
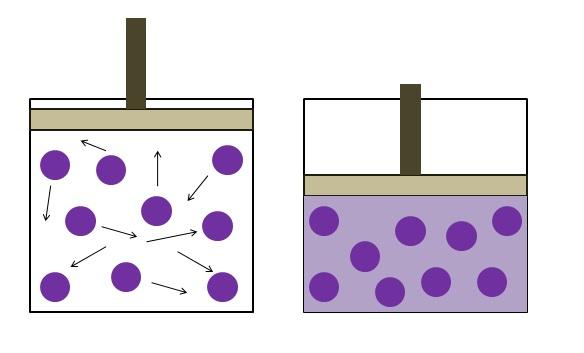
Fue formulada independientemente por el físico Robert Boyle (1662) y el físico y botánico Edme Mariotte (1676). La ley se enuncia en la forma siguiente: a temperatura constante, el volumen de una masa fija de un gas es inversamente proporcional a la presión que este ejerce.
PV ∝ k
Mediante el uso de dos puntos:
P1V1 = P2V2
Ley de Charles-Gay-Lussac

La ley fue publicada por Gay-Lussac en 1803, pero hacía referencia al trabajo no publicado por Jacques Charles (1787). Por esta razón la ley es conocida como ley de Charles.
La ley establece que a presión constante, existe una relación directa de proporcionalidad entre el volumen ocupado por un gas y su temperatura.
V ∝ k2T
Mediante el uso de dos puntos:
V1/T1 = V2/T2
V1T2 = V2T1
Ley de Avogadro
La ley fue enunciada por Amadeo Avogadro en 1811, señalando que volúmenes iguales de todos los gases, a la misma presión y temperatura, tienen el mismo número de moléculas.
V1/n1 = V2/n2
Mediante la ley de los gases ideales se establece una relación entre cuatro propiedades físicas independientes del gas: la presión, el volumen, la temperatura y la cantidad del gas. Basta con conocer el valor de tres de ellas, para poder obtener el de la restante.
La Ley establece las condiciones que señalan cuándo un gas se comporta idealmente, y cuándo se aleja de este comportamiento.
Por ejemplo, el llamado factor de compresión (PV/nRT) tiene un valor de 1 para los gases ideales. Un alejamiento del valor de 1 para el factor de compresión, indica que el comportamiento del gas se aleja del mostrado por un gas ideal.
Por lo tanto, se cometería un error al aplicar la ecuación de los gases ideales a un gas que no se comporta de acuerdo al modelo.
La ecuación de la ley de gases ideales puede utilizarse en el cálculo de la densidad de un gas y de su masa molar. Al hacerle una modificación simple, se puede hallar una expresión matemática que relacione la densidad (d) de un gas y su masa molar (M):
d = MP/RT
Y despejando M:
M = dRT/P
La estequiometria es la rama de la química que relaciona la cantidad de cada uno de los reactivos presentes con los productos que intervienen en una reacción química, generalmente expresados en moles.
El uso de la ecuación de los gases ideales permite la determinación del volumen de un gas producido en una reacción química; ya que, de la reacción química se puede obtener el número de moles. Luego, se puede calcular el volumen del gas:
PV = nRT
V = nRT/P
Midiendo V puede determinarse el rendimiento o avance de dicha reacción. Cuando no haya más gases, es indicativo de que los reactivos se han agotado por completo.
La Ley de los gases ideales puede ser utilizada, conjuntamente con la ley de las presiones parciales de Dalton, para calcular las presiones parciales de los diferentes gases presentes en una mezcla de gases.
Se aplica la relación:
P = nRT/V
Para la hallar la presión de cada uno de los gases presentes en la mezcla.
Se realiza una reacción que produce un gas, el cual es recogido mediante un diseño experimental en agua. Se conoce la presión total del gas más la presión de vapor de agua. El valor de esta última puede ser obtenida en una tabla y por sustracción se puede calcular la presión del gas.
De la estequiometria de la reacción química se puede obtener el número de moles del gas, y aplicando la relación:
V = nRT/P
Se calcula el volumen del gas producido.
Un gas tiene una densidad de 0,0847 g/L a 17 ºC, y una presión de 760 torr. ¿Cuál es su masa molar? ¿Cuál es el gas?
Partimos de la ecuación
M = dRT/P
Convertimos primero las unidades de temperatura a kelvin:
T = 17 ºC + 273,15 K = 290,15 K
Y la presión de 760 torr corresponde a la de 1 atm. Ahora solamente hace falta sustituir los valores y resolver:
M = (0,0847 g/L)(0,08206 L·atm·K-1·mol-1)(290,15 K) / 1 atm
M = 2,016 g/mol
Esta masa molar puede corresponder a una única especie: la molécula diatómica de hidrógeno, H2.
Una masa de 0,00553 g de mercurio (Hg) en fase gaseosa, se encuentra en un volumen de 520 L, y a una temperatura de 507 K. Calcular la presión ejercida por el Hg. La masa molar del Hg es 200,59 g/mol.
El problema se resuelve mediante el uso de la ecuación:
PV = nRT
No aparece la información acerca del número de moles de Hg; pero se pueden obtener mediante el uso de su masa molar:
Número moles de Hg = (0,00553 g de Hg) (1 mol Hg/200,59 g)
=2,757·10-5 moles
Ahora solo tenemos que despejar P y sustituir los valores:
P = nRT/V
= (2,757·10-5 moles)(8,206·10-2 L·atm·K-1·mol-1)(507 K)/ 520 L
= 2,2·10-6 atm
Calcular la presión generada por el ácido clorhídrico producido al reaccionar 4,8 g de gas cloro (Cl2) con el gas hidrógeno (H2), en un volumen de 5,25 L, y a una temperatura de 310 K. La masa molar del Cl2 es 70,9 g/mol.
H2(g) + Cl2(g) → 2 HCl(g)
El problema se resuelve mediante el uso de la ecuación de los gases ideales. Pero la cantidad de HCl está expresada en gramos y no en moles, por lo que se hace la transformación debida.
Moles de HCl = (4,8 g Cl2) (1 mol de Cl2/70,9 g Cl2) (2 mol de HCl/1mol de Cl2)
= 0,135 moles de HCl
Aplicando la ecuación de la ley de los gases ideales:
PV = nRT
P = nRT/V
= (0,135 moles de HCl)(0,08206 L·atm·K-1·mol-1)(310 K) / 5,25 L
= 0,65 atm
Una muestra de 0,130 g de un compuesto gaseoso ocupa un volumen de 140 mL a una temperatura de 70 ºC y a una presión de 720 torr. ¿Cuál es su masa molar?
Para aplicar la ecuación de los gases ideales, debe hacerse primero varios cambios:
V = (140 mL) (1 L/1000 mL)
= 0,14 L
Teniendo el volumen en litros, ahora hay que expresar la temperatura en kelvin:
T = 70 ºC + 273,15 K = 243,15 K
Y por último, debemos convertir la presión en unidades de atmósfera:
P = (720 torr) (1 atm/760 torr)
= 0,947 atm
El primer paso en la resolución del problema es obtener el número de moles del compuesto. Para ello se usa la ecuación de los gases ideales y despejamos n:
PV = nRT
n = PV / RT
= (0,947 atm) (0,14 L) / (0,08206 L·atm·K-1·mol-1) (243,15 K)
= 0,067 moles
Solamente hace falta calcular la masa molar dividiendo los gramos entre los moles obtenidos:
Masa molar = gramos del compuesto / número de moles.
= 0,130 g / 0,067 moles
= 19,49 g/mol
- Whitten, Davis, Peck & Stanley. (2008). Química. (8va ed.). CENGAGE Learning.
- Ira N. Levine. (2014). Principios de Fisicoquímica. Sexta edición. Mc Graw Hill.
- Glasstone. (1970). Tratado de química física. Segunda edición. Aguilar.
- Mathews, C. K., Van Holde, K. E., y Ahern, K. G. (2002). Bioquímica. 3era Edición. Editorial Pearson Addison Wesley.
- Wikipedia. (2019). Ideal gas. Recuperado de: en.wikipedia.org
- Equipo Editorial. (2018). Ley de Boyle o ley de Boyle-Mariotte | Leyes de los gases. Recuperado de: iquimicas.com
- Jessie A. Key. (s.f.). The Ideal Gas Law and Some Applications. Recuperado de: opentextbc.ca
