Energía potencial: características, tipos, cálculo y ejemplos

La energía potencial es la energía que los cuerpos poseen en virtud de su configuración. Cuando los objetos interactúan, existen entre ellos fuerzas capaces de realizar trabajo, y esta capacidad de hacer trabajo, que se almacena en la disposición que tienen, puede traducirse en energía.

Por ejemplo, los seres humanos han aprovechado la energía potencial de las caídas de agua desde tiempos inmemoriales, primero haciendo girar molinos y luego en centrales hidroeléctricas.

Por otro lado, muchos materiales tienen una notable capacidad de hacer trabajo al deformarse y regresar luego a su tamaño original. Y en otras circunstancias, la disposición de la carga eléctrica permite almacenar energía potencial eléctrica, como por ejemplo en un condensador.

La energía potencial ofrece muchísimas posibilidades para transformarse en otras formas de energía aprovechables, de allí la importancia de conocer las leyes que la rigen. 

Índice del artículo

• 1 Origen de la energía potencial
• 2 Tipos de energía potencial
  • 2.1 Energía potencial gravitatoria
  • 2.2 Energía potencial elástica
  • 2.3 Energía potencial electrostática
  • 2.4 Energía potencial nuclear
  • 2.5 Energía potencial química
• 3 Ejemplos de energía potencial
• 4 Cálculo de la energía potencial
  • 4.1 Cálculo de la energía potencial gravitacional
  • 4.2 Cálculo de la energía potencial elástica
  • 4.3 Cálculo de la energía potencial electrostática
• 5 Ejercicios resueltos
  • 5.1 – Ejercicio 1: un resorte que se estira
  • 5.2 – Ejercicio 2: fuerzas conservativas y no conservativas
• 6 Referencias

Origen de la energía potencial

La energía potencial de un objeto tiene su origen en las fuerzas que lo afectan. Sin embargo, la energía potencial es una magnitud escalar, mientras que las fuerzas son vectoriales. Por ello, para especificar la energía potencial, basta con indicar su valor numérico y las unidades seleccionadas.

Otra cualidad importante es el tipo de fuerza con el que se puede almacenar energía potencial, ya que no cualquier fuerza tiene esta virtud. Solamente las fuerzas conservativas almacenan energía potencial en los sistemas sobre los cuales actúan.

Una fuerza conservativa es aquella para la cual el trabajo no depende de la trayectoria seguida por el objeto, sino solamente del punto de partida y del punto de llegada. La fuerza que impulsa la caída del agua es la gravedad, que es una fuerza conservativa.

Por otro lado, las fuerzas elásticas y electrostáticas también poseen esta cualidad, por lo tanto hay energía potencial asociada a ellas.

A las fuerzas que no cumplen el requisito mencionado, se las llama no conservativas; ejemplo de ellas se tienen en el rozamiento y la resistencia del aire.

Tipos de energía potencial

Puesto que la energía potencial deriva siempre de fuerzas conservativas como las ya mencionadas, se habla de energía potencial gravitatoria, energía potencial elástica, energía potencial electrostática, energía potencial nuclear y energía potencial química.

Energía potencial gravitatoria

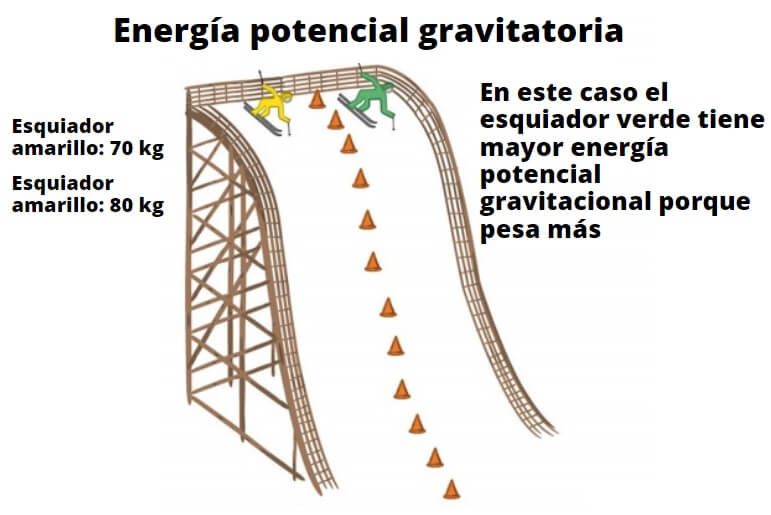
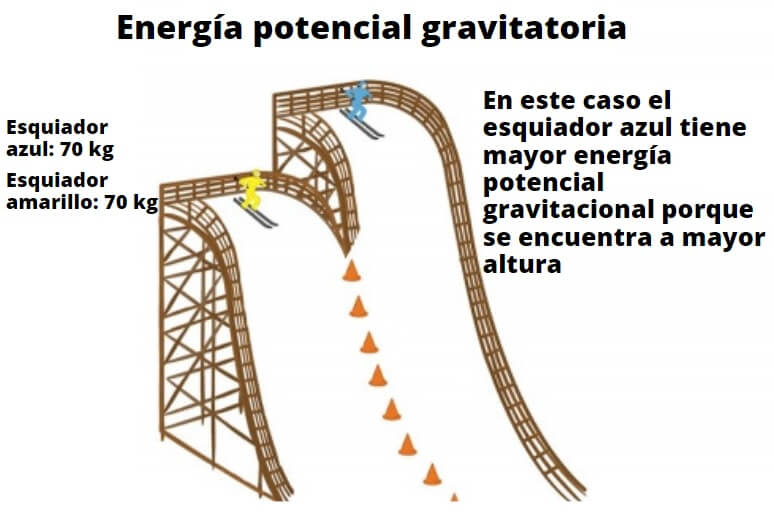
Cualquier objeto posee energía potencial en función de la altura que tienen respecto al suelo. Este hecho tan simple en apariencia, ilustra porque la caída de agua es capaz de impulsar turbinas y transformarse eventualmente en energía eléctrica. El ejemplo de los esquiadores que se muestra aquí también muestra la relación del peso y la altura con la energía potencial gravitatoria.

Otro ejemplo es el de un vagón de montaña rusa, el cual tiene mayor energía potencial cuando se encuentra a cierta altura sobre el suelo. Una vez que ha llegado al nivel del piso, su altura es igual a cero y toda su energía potencial se ha transformado en energía cinética (energía de movimiento).

Energía potencial elástica

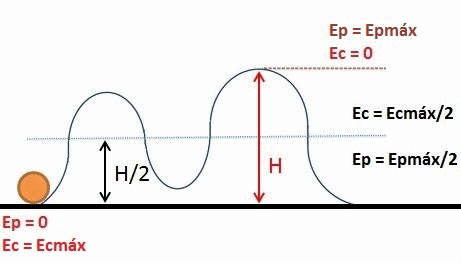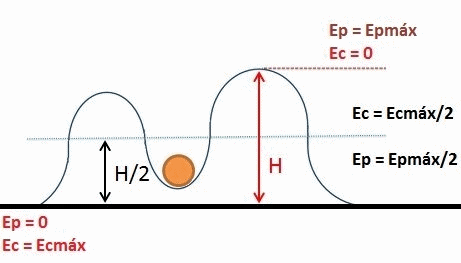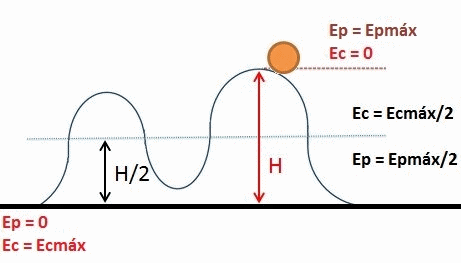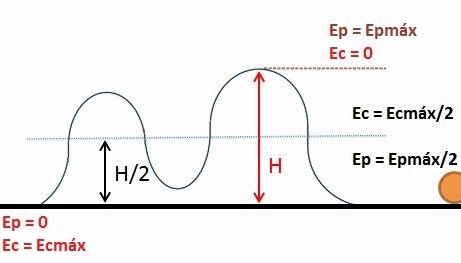
Objetos tales como resortes, arcos, ballestas y ligas son capaces de almacenar energía potencial elástica.

La elasticidad de un cuerpo o de un material se describe mediante la ley de Hooke (hasta ciertos límites), que nos dice que la fuerza capaz de ejercer cuando está comprimido o estirado, es proporcional a su deformación.

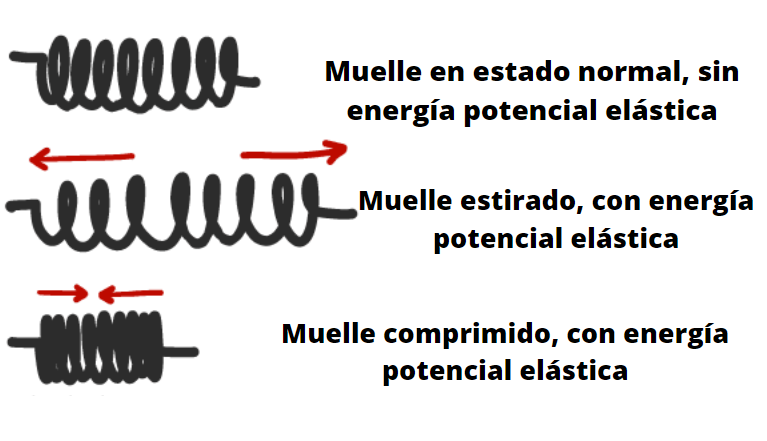
Por ejemplo en caso de un resorte o muelle, esto significa que cuanto más se encoge o se estira, mayor es la fuerza que puede ejercer sobre un objeto colocado en un extremo.

Energía potencial electrostática

Es la energía que tienen las cargas eléctricas en virtud de su configuración. Las cargas eléctricas del mismo signo se repelen, así que para colocar un par de cargas positivas -o negativas- en cierta posición, un agente externo debe hacer trabajo. De lo contrario ellas tenderían a separarse.

Este trabajo queda almacenado en el modo en que quedaron ubicadas las cargas. Cuanto más cercanas estén las cargas del mismo signo, mayor energía potencial tendrá la configuración. Sucede al contrario cuando se trata de cargas de signos diferentes; como ellas se atraen, cuanto más cerca estén, menos energía potencial tienen.

Energía potencial nuclear

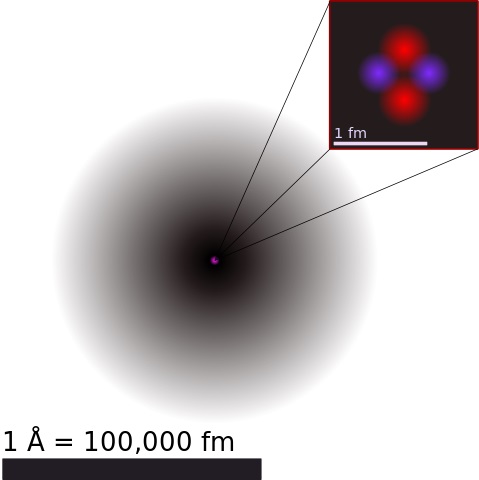
El núcleo atómico está compuesto protones y neutrones, denominados genéricamente nucleones. Los primeros tienen carga eléctrica positiva y los segundos son neutros.

Puesto que están aglomerados en un espacio diminuto más allá de la imaginación, y sabiendo que las cargas del mismo signo se repelen, cabe preguntarse cómo el núcleo atómico se mantiene cohesionado.

La respuesta está en otras fuerzas además de la repulsión electrostática, propias del núcleo, como son la interacción nuclear fuerte y la interacción nuclear débil. Se trata de fuerzas muy intensas, que superan con creces a la fuerza electrostática.

Energía potencial química

Esta forma de energía potencial proviene de la cómo se disponen los átomos y las moléculas de las sustancias, de acuerdo a los distintos tipos de enlaces químicos.

Cuando se da una reacción química, esta energía puede transformarse en otros tipos, por ejemplo mediante una pila o batería eléctrica.

Ejemplos de energía potencial

La energía potencial está presente en la vida diaria en muchísimos aspectos. Observar sus efectos es tan fácil como colocar cualquier objeto a cierta altura y tener la certeza de que puede rodar o caer en cualquier momento.

A continuación algunas manifestaciones de los tipos de energía potencial descritos previamente:

-Montañas rusas

-Automóviles o pelotas rodando cuesta abajo

-Arcos y flechas

-Baterías eléctricas

-Un péndulo de reloj

-Balancearse en un columpio

-Saltar en un trampolín

-Usar un bolígrafo retráctil.

Ver: ejemplos de energía potencial.

Cálculo de la energía potencial

La energía potencial depende del trabajo que haga la fuerza y este a su vez no depende de la trayectoria, entonces se puede afirmar que:

-Si  A y B son dos puntos, el trabajo W_AB  necesario para ir desde A hasta B, es igual al trabajo necesario para ir de B hasta A. Por lo tanto: W_AB = W_BA, así que:

W_AB + W_BA = 0

-Y si se prueban dos trayectorias diferentes 1 y 2 para unir dichos puntos A y B, el trabajo hecho en ambos casos también es el mismo:

 W₁ = W₂.

En cualquier caso el objeto experimenta un cambio en la energía potencial:

Cambio = Energía potencial final – Energía potencial inicial

ΔU = U_final – U_inicial = U_B – U_A

Pues bien, la energía potencial del objeto se define como el negativo del trabajo realizado por la fuerza (conservativa):

ΔU = -W_AB

Pero como el trabajo se define mediante esta integral:

Nótese que las unidades de la energía potencial, son las mismas que las del trabajo. En el Sistema Internacional SI la unidad es el joule, que se abrevia J y equivale a 1 newton x metro, por el físico inglés James Joule (1818-1889).

Otras unidades para la energía incluyen el ergio en el sistema cgs, la libra-fuerza x pie, el BTU (British Thermal Unit), las calorías y el kilowatt-hora.

Veamos seguidamente algunos casos particulares de cómo calcular la energía potencial.

Cálculo de la energía potencial gravitacional

En las cercanías de la superficie terrestre, la fuerza de gravedad apunta verticalmente hacia abajo y su magnitud viene dada por la ecuación Peso = masa x gravedad.

Denotando el eje vertical con la letra “y” y asignando a esta dirección el vector unitario j, positivo hacia arriba y negativo hacia abajo, el cambio en la energía potencial cuando un cuerpo se desplaza desde y = y_A hasta y = y_B es:

U(y) = mgy

Cálculo de la energía potencial elástica

La ley de Hooke nos dice que la fuerza es proporcional a la deformación:

F = -k.x

Aquí x es la deformación y k es una constante propia del resorte, que indica cuán rígido es. Mediante esta expresión se calcula la energía potencial elástica, tomando en cuenta que i es el vector unitario en la dirección horizontal:

U(x) = ½ kx²

Cálculo de la energía potencial electrostática

Cuando se tiene una carga eléctrica puntual Q, ésta produce un campo eléctrico que percibe otra carga puntual q, y que hace trabajo sobre ésta cuando se la mueve desde una posición a otra en medio del campo. La fuerza electrostática entre dos cargas puntuales tiene dirección radial, simbolizada a través del vector unitario r:

Ejercicios resueltos

– Ejercicio 1: un resorte que se estira

Un resorte cuya constante es k = 10.0 N/cm se estira inicialmente 1.00 cm desde su longitud de equilibrio. Se pide calcular la energía adicional necesaria para estirar el resorte hasta 5.00 cm más allá de su longitud de equilibrio.

Solución 

Sustituyendo directamente x = 1.00 cm en la ecuación para U(x) se obtienen N.cm, pero los centímetros deben convertirse a metros para obtener la energía en joules:

U(1) = 0.5 x 10.0 N/cm x (1.00 cm)² = 5 N. cm = 0.05 J; U (5) = 0.5 x 10.0 N/cm x (5.00 cm)² = 125 N.cm = 1.25 J

Por lo tanto la diferencia de energía buscada es 1.25 – 0.05 J = 1.20 J.

– Ejercicio 2: fuerzas conservativas y no conservativas

Se suelta desde el reposo un pequeño bloque desde el punto A, para que deslice a lo largo de la rampa curva sin fricción hasta el punto B. A partir de allí ingresa a una larga superficie horizontal áspera, con un coeficiente de fricción dinámica μ_k = 0.2. Encontrar a qué distancia del punto B se detiene, suponiendo que h_A= 3m.

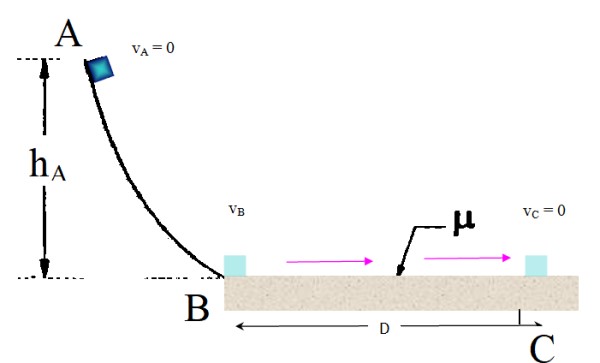
Solución 

Cuando el bloque se encuentra a una altura h_A respecto al piso, posee energía potencial gravitatoria debido a su altura. Al soltarse, esta energía potencial se convierte poco a poco en energía cinética, y a medida que resbala por la rampa curvada lisa, su rapidez va aumentando.

Durante el trayecto que va desde A hasta B, no se pueden aplicar las ecuaciones del movimiento rectilíneo uniformemente variado. Si bien la gravedad es la responsable del movimiento del bloque, el movimiento que este experimenta es más complejo, debido a que la trayectoria no es rectilínea.

Conservación de la energía en el trayecto AB

Sin embargo, como la gravedad es una fuerza conservativa y en la rampa no hay rozamiento, se puede utilizar la conservación de la energía mecánica para encontrar la rapidez al llegar al final de la rampa:

Energía mecánica en A = Energía mecánica en B

m.g.h_A + ½ m.v_A² = m.g.h_B + ½ m.v_B²

La expresión se simplifica notando que la masa aparece en cada término. Se suelta del reposo v_A = 0. Y h_B está a nivel del suelo, h_B = 0. Con estas simplificaciones, la expresión se reduce a:

v_B² = gh_A

Trabajo hecho por el roce en el tramo BC

Ahora el bloque inicia su recorrido en el tramo áspero con esta velocidad y finalmente se detiene en el punto C. Por lo tanto v_C = 0. La energía mecánica ya no se conserva, porque el rozamiento es una fuerza disipativa, que ha hecho un trabajo sobre el bloque dado por:

W_roce = -fuerza de roce x distancia recorrida

Este trabajo tiene signo negativo, ya que el roce cinético frena al objeto, oponiéndose a su movimiento. La magnitud del roce cinético f_k  es:

f_k = μ_k .N

Donde N es la magnitud de la fuerza normal. La fuerza normal es ejercida por la superficie sobre el bloque, y como la superficie es totalmente horizontal, pues equilibra al peso P = mg, por lo tanto la magnitud de la normal es:

N = mg

Lo que lleva a:

f_k = μ_k .mg

El trabajo que f_khace sobre el bloque es: W_k = – f_k .D =- μ_k .mg.D.

Cálculo del cambio en la energía mecánica

Este trabajo equivale al cambio en la energía mecánica, calculado así:

Energía mecánica en C – Energía mecánica en B =

ΔE_m = (U_C +K_C)- (U_B + K_B)= – μ_k .mg.D

En esta ecuación hay algunos términos que se anulan: K_C = 0, ya que el bloque se detiene en C y también se anulan U_C = U_B, por estar estos puntos a nivel del suelo. La simplificación resulta en:

– K_B = – μ_k .m.g.D

½ m.v_B² = μ_k .m.g.D

La masa nuevamente se cancela y se puede obtener D de la siguiente manera:

D = (½ v_B²)/( μ_k . g) = (½ v_B²)/( μ_k . g)= (½g.h_A)/(μ_k . g) =(½h_A)/μ_k = 0.5 x 3 m / 0.2 = 7.5 m

Referencias

1. Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
2. Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 2. Dinámica. Editado por Douglas Figueroa (USB).
3. Giancoli, D.  2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
4. Knight, R.  2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson. 
5. Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1-2.