Ley de Hooke: fórmulas, ejemplos, aplicaciones, ejercicios
La ley de Hooke señala que la deformación experimentada por un objeto elástico es directamente proporcional a la fuerza aplicada sobre él. La constante de proporcionalidad depende de la naturaleza del objeto, su geometría y el material con que esté fabricado.
Todos los materiales tienen propiedades elásticas en mayor o menor medida, así que cumplen la ley de Hooke siempre que regresen a sus dimensiones originales, una vez que cesa la fuerza. Los resortes y las gomas elásticas son buenos ejemplos de objetos que cumplen la ley de Hooke, pero también lo son las cabillas de acero que forman parte de un puente.

Tomando como ejemplo un resorte o muelle, para mantenerlo estirado o comprimido, es necesario aplicar una fuerza cuya magnitud es F. De acuerdo a la ley de Hooke, el resorte experimentará una deformación x:
F ∝ x
La constante de proporcionalidad, que al tratarse de un resorte se llama constante de rigidez del resorte, se denota como k, por lo tanto:
F = k⋅x
En las unidades del Sistema Internacional, la fuerza viene en newton (N) y la deformación en metros (m). Por lo tanto, la constante del resorte tiene unidades de N/m. La constante del resorte representa la fuerza que se debe aplicar para deformarlo en 1 m de longitud.
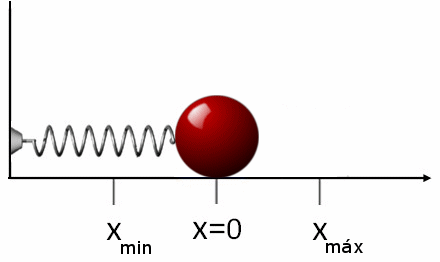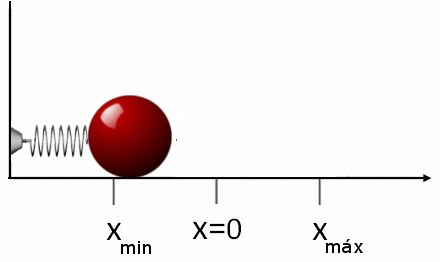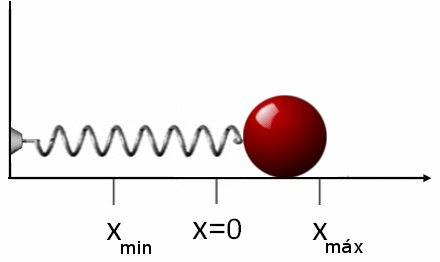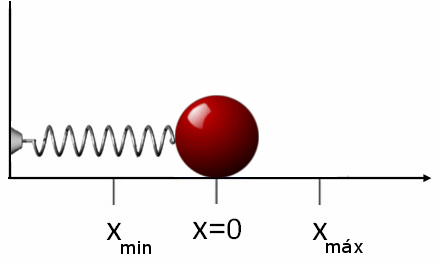
Si luego de estirar o comprimir el resorte se le suelta, este se desplazará en dirección contraria a la fuerza aplicada. Esto quiere decir que si lo estiramos, se comprime y viceversa. Por eso la fuerza FR que el resorte ejerce es:
FR = -k⋅x
El signo negativo indica lo antes dicho: que la fuerza se opone al desplazamiento, por ello a esta fuerza se la conoce como fuerza restauradora.
Índice del artículo
- 1 Fórmula y ecuaciones
- 2 Ejemplos de resortes
- 3 Aplicaciones de la ley de Hooke
- 4 Ejercicios resueltos
- 5 Referencias
La relación entre la fuerza y el desplazamiento en un resorte fue descubierta por Robert Hooke (1635-1703), notable físico inglés y conocido por su rivalidad con Isaac Newton. Hooke fue un científico versátil que incursionó con éxito en distintos campos de la ciencia: la mecánica, la biología, la astronomía y la arquitectura.

Hooke se percató de que si la fuerza aplicada a un muelle no es muy grande, el muelle se deforma proporcionalmente a la fuerza, y una vez que dicha fuerza desaparece, el resorte vuelve a tener su longitud natural.
De esta forma, la ley de Hooke en forma gráfica tiene la forma de una línea recta, cuya pendiente es la constante del resorte. En la siguiente imagen se muestra la fuerza que se ejerce sobre el resorte para estirarlo –o comprimirlo- en función de la posición x. Nótese también que la fuerza no depende de la longitud natural del resorte, sino de su desplazamiento.
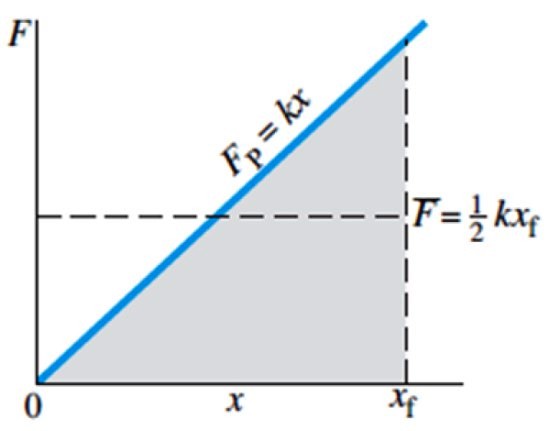
La fuerza promedio se indica en la gráfica mediante la F con barra y equivale a ½ kxf, donde xf es la posición final del resorte.
Tanto la fuerza que se ejerce sobre el resorte, como la fuerza que él ejerce sobre un objeto atado a él, son fuerzas variables. Mientras más se quiera estirar o comprimir al resorte, más fuerza hay que aplicar para poder lograrlo.
Cuando se aplica una fuerza que deforma al resorte, se hace un trabajo que queda almacenado en el resorte y que se puede utilizar después.
El trabajo mecánico se define como el área bajo la gráfica de la fuerza F en función de la posición x. Para calcular el trabajo W que una fuerza variable F(x) hace al mover un objeto desde la posición x1 hasta la posición x2 hay que calcular la integral definida:
En el caso del trabajo necesario para llevar un resorte desde su posición de equilibrio hasta la posición xf es muy sencillo, ya que el área a calcular es la del triángulo sombreado en gris de la figura 4, cuya fórmula es conocida:
Área del triángulo = ½ base. altura
Por lo tanto el trabajo necesario es:
W = ½ xf . (kxf) = ½ k (xf)2
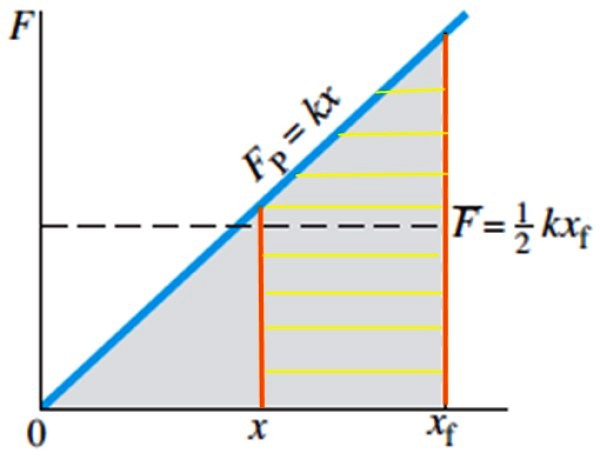
Y si se quiere calcular el trabajo necesario para llevar al resorte desde la posición x hasta la posición xf, sería equivalente a calcular el área del trapecio rayado de la figura 5:
W = ½ k (xf)2 – ½ k x2
Según la aplicación a la que estén destinados, los resortes pueden ser helicoidales cilíndricos, cónicos, en espiral, con sección transversal circular (los más comunes), de sección cuadrada o rectangular.
Una clasificación muy usada es según el tipo de esfuerzo al que vayan a ser sometidos: hay resortes de torsión, de flexión, de compresión y de extensión. Estos últimos se utilizan extensivamente y los hay que funcionan igualmente para tensión y compresión.
Un ejemplo de resorte de compresión es el que se usa en el juguete llamado pogo o palo saltarín. Estos resortes almacenan bastante energía potencial cuando se comprimen y la van liberando poco a poco mientras regresan a la posición de equilibrio. De esta forma los rebotes no son demasiado bruscos.

Los resortes para trampolines son el tipo de resortes de extensión y se fabrican con espiras bien enrolladas, con dos ganchos en los extremos. Son capaces de retener bastante energía potencial, que luego liberan cuando alguien sube y comienza a saltar sobre la lona, que también tiene su propia respuesta elástica, como todos los materiales.
Los resortes de torsión son muy comunes, porque sirven para hacer pinzas de ropa. En vez de ganchos en los extremos, estos se doblan en ángulo, para resistir las fuerzas que tienden a ejercer torsión.

Los materiales más idóneos para fabricar resortes son aquellos con una resistencia última (resistencia final) elevada, es decir, que soportan un gran esfuerzo antes de romperse. También es conveniente que el material tenga un alto punto de fluencia, para que no pierda sus cualidades elásticas con esfuerzos pequeños.
Los resortes de uso industrial se fabrican con aleaciones que incluyen el acero con alto contenido de carbono, cobre, níquel y bronce.
Como los resortes tienen la virtud de almacenar energía potencial cuando se estiran o comprimen, son capaces de realizar trabajo moviendo cosas como mecanismos.
De esta manera los resortes tienen multitud de aplicaciones, desde objetos pequeños y cotidianos, pasando por los automóviles, hasta maquinarias de todo tipo. Los resortes sirven para:
-Amortiguar vibraciones.
-Fabricar mecanismos retráctiles: bolígrafos, pinzas de colgar ropa, ganchos para el cabello.
-Hacer balanzas de muelle o dinamómetros
Y también forman parte del mecanismo de:
-Relojes.
-Trampolines.
-Cerraduras.
-Juguetes.
-Armas.
-Medidores de aguja, por ejemplo el galvanómetro, usado para medir corrientes, voltajes y resistencias.
Se aplica una fuerza de magnitud 5.0 N a un resorte, logrando que se estire una longitud de 3.5 cm a partir de su longitud natural.
a) ¿Qué tanto se estira cuando la fuerza aplicada es de 7 N?
b) Encuentre el trabajo que realiza la fuerza aplicada para estirar al resorte 3.5 cm a partir de su longitud natural.
Solución a
Sabiendo que el resorte se estira 3.5 cm mediante la aplicación de 5.0 N podemos calcular su constante:
k = F / x = 5.0 N / 3.5 cm = 1.43 N / cm.
Cuando se aplica una fuerza de 7 N, se obtiene el siguiente estiramiento:
x = F / k = 7.0 N / 1.43 N/m = 4.9 cm
Solución b
El trabajo necesario para deformar un resorte viene dado por:
W = ½ kx2 = 0.5 x 1.43 N / cm x (3.5 cm)2 = 8.76 N . cm = 8.76 N . 1 x10 -2 m = 0.0876 J.
Un resorte de masa despreciable y 10 cm de largo pende de un soporte. Si se le cuelga una masa de 2 kg, el resorte se estira hasta alcanzar 15 cm. Calcular:
a) La constante del resorte
b) El tamaño del resorte cuando se suspende una masa de 3 kg.
Solución a
El estiramiento del resorte es de x = 15 – 10 cm = 5 cm
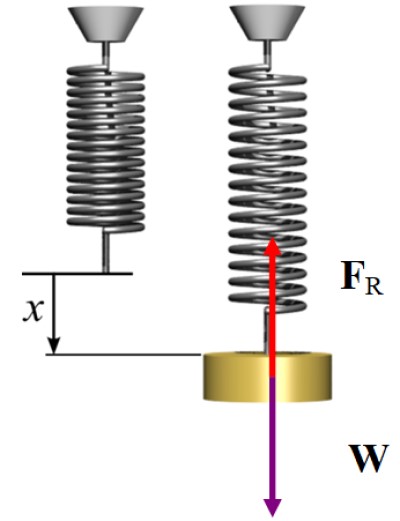
Como el sistema se encuentra en equilibrio estático, la fuerza que ejerce el resorte al estirarse se dirige verticalmente hacia arriba, para compensar al peso, que va dirigido hacia abajo, entonces:
FR = W → kx = mg
k = 2 x 9.8 N / 5 x10 -2 m = 392 N/m
Solución b
Cuando se suspende una pesa de 3 kg, la nueva fuerza es W = 3 x 9.8 N = 29.4 N
En tal caso el estiramiento es:
x = mg /k = 29. 4 N / 392 N/m = 0.075 m = 7.5 cm
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Creative Mechanisms Blog. Four different types of springs. Recuperado de: creativemechanisms.com.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 2. Dinámica. Editado por Douglas Figueroa (USB).
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed. Prentice Hall.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
