Teorema de Bernoulli: concepto, ecuación, aplicaciones, ejercicio

¿Qué es el teorema de Bernoulli?

El teorema de Bernoulli afirma que, en un fluido ideal circulando en estacionariamente por un conducto, la energía mecánica por unidad de volumen del fluido es constante en todo los tramos del tubo, sin importar que tengan distinta sección transversal de área y altura.

Ahora bien, un fluido ideal es aquel que no puede comprimirse, por lo que su densidad es fija, independientemente del valor de la presión.

Además un fluido ideal tiene viscosidad nula, es decir, no hay fricción entre las capas de fluido y tampoco entre el fluido y las paredes del conducto.

Las condiciones de incompresibilidad y viscosidad nula son imprescindibles para aplicar el teorema de Bernoulli. También es necesario que el flujo sea estacionario, esto es, el caudal no varía con el tiempo.

Por otra parte el flujo debe ser laminar, así que no puede haber remolinos ni turbulencias durante el paso del fluido por el conducto.

Ecuación de Bernoulli

La ecuación de Bernoulli es:

Por otra parte, la ecuación de continuidad establece que en un fluido ideal el caudal es constante en todas las secciones del tubo de flujo. Es decir, el volumen de fluido en una misma unidad de tiempo es igual en todas las secciones del tubo.

Si el caudal es Q, entonces:

Q = constante

Con:

Q = A·v

Donde A es el área de sección transversal del tubo y v es la velocidad del fluido.

Se advierte que en las secciones más estrechas del tubo, el fluido debe circular con mayor rapidez, ya que Q se mantiene constante aunque A varíe. Por lo tanto, la energía cinética por unidad de volumen es mayor.

Dado que el teorema de Bernoulli establece que la energía mecánica es constante en todas las secciones, en las secciones estrechas de mayor energía cinética la energía potencial disminuye. 

La energía potencial consta de la energía gravitatoria por unidad de volumen más el trabajo realizado por la presión en un volumen unitario, por tanto, al decrecer la energía potencial también decrece la presión.

En resumen, el efecto combinado del principio de continuidad y el teorema de Bernoulli trae como consecuencia que en las secciones estrechas del tubo de flujo, donde la velocidad del fluido es mayor, la presión descienda respecto a las secciones más anchas.

Términos en la ecuación de Bernoulli

1) Trabajo realizado por la presión por unidad de volumen 

En un tramo de sección transversal de área A, el fluido se desplaza una cantidad s, a causa de la presión P que produce una fuerza F = P⋅ A.

El trabajo realizado por la fuerza es:

F⋅ s = P⋅ A⋅ s

Como el producto A⋅s representa el volumen desplazado, entonces el trabajo realizado por unidad de volumen coincide numéricamente con el valor de P en el tramo considerado.

2) Energía cinética de un volumen unitario de fluido

Como el fluido es incompresible, su densidad tiene un valor fijo llamado ρ.

Cuando circula el fluido por un tramo de sección transversal A, desplazándose una cantidad s en un tiempo t, la velocidad del flujo es:

v = s/t

Y la energía cinética de dicha porción de fluido se calcula mediante:

K = ½ ρ (A⋅s) v²

Pero si el volumen desplazado (A⋅s) es unitario, entonces el término de energía cinética estará dado por ½ ρ v².

3) Energía potencial gravitacional de un volumen unitario de fluido a una altura h 

Para una porción de fluido de masa m y altura h respecto a determinado nivel de referencia, la energía gravitacional está dada por:

U = m⋅ g⋅ h

Si la masa m corresponde a una porción unitaria de fluido, entonces la masa de la porción coincide numéricamente con la densidad ρ, por lo que la energía potencial será ρ⋅ g⋅ h.

Aplicaciones del teorema de Bernoulli

Sustentación aerodinámica

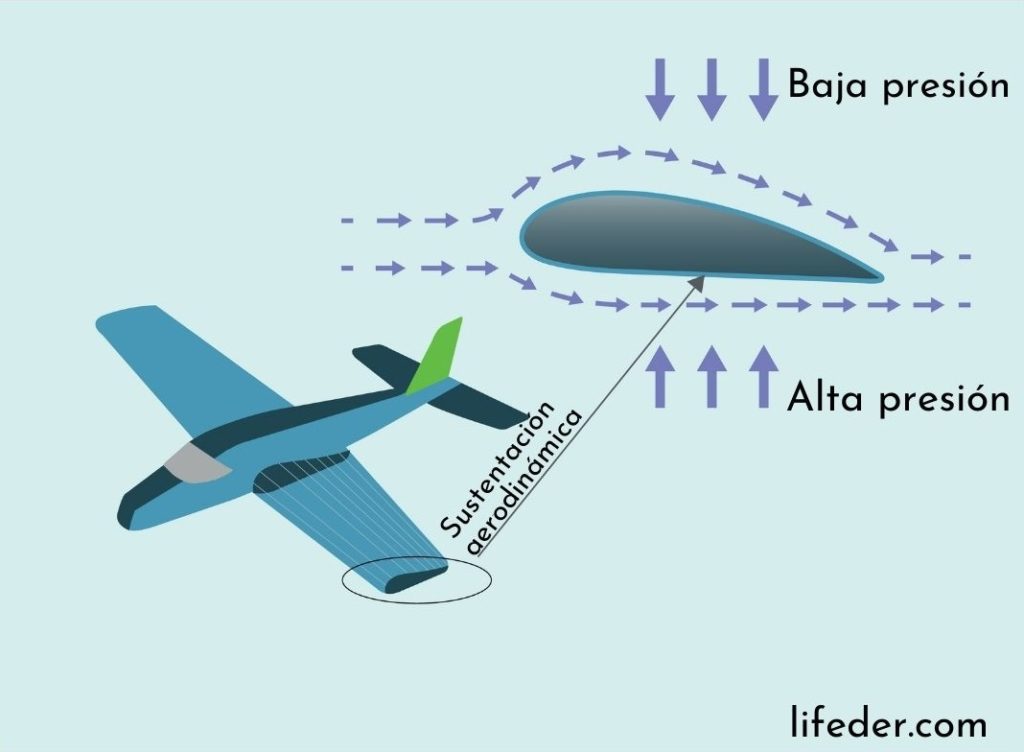
La fuerza que impide que un avión en vuelo se desplome hacia tierra es la fuerza de sustentación aerodinámica. La fuerza de sustentación neta va dirigida verticalmente hacia arriba y actúa a lo largo del ala del avión. Su origen se explica a través del teorema de Bernoulli.

El ala de un avión tiene una sección transversal con una curva más larga en la parte superior y más corta en la parte inferior. Esto hace que el recorrido del aire cerca de la superficie del ala sea mayor en la parte superior, por lo que el aire fluye más rápidamente encima del ala que por la parte de abajo. 

Como consecuencia del teorema de Bernoulli, la presión del aire en la parte alta del ala  circulante es menor que en la parte inferior, dando como resultado que la fuerza ejercida por la diferencia de presiones esté dirigida hacia arriba, sustentando el peso del avión, según se aprecia en la siguiente imagen.

Lanzamiento de balones y pelotas con efecto de curva

En algunos deportes como fútbol, béisbol y cricke, los jugadores experimentados saben hacer lanzamientos de forma tal que la trayectoria de la pelota se curva en forma inesperada, confundiendo al oponente. Es lo que se llama lanzamiento con efecto.

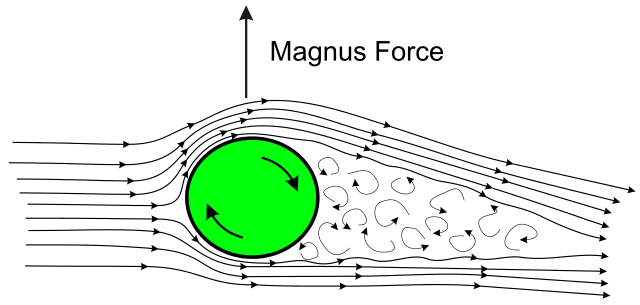
El efecto se produce siempre que la pelota o balón vaya girando rápidamente mientras se desplaza por el aire. La rotación hace que el aire aledaño a la superficie de la pelota sea arrastrado por la misma en dos direcciones opuestas, una a favor de la dirección de traslación y, por la otra cara, en contra de la dirección de desplazamiento.

A consecuencia del arrastre de aire, en una cara de la pelota se produce una zona de baja presión y en la cara opuesta una de alta presión, produciendo una fuerza neta que desvía la trayectoria natural de la pelota.

La explicación de este fenómeno conocido como efecto Magnus reside justamente en el teorema de Bernoulli: por donde el fluido circula rápido la presión es baja, y por el lado donde circula lento la presión es alta.

Ejercicio resuelto

Un tubo horizontal tiene una sección de área A₁ = 40 centímetros cuadrados y otro tramo de sección de área A₂ cuatro veces menor. Si el flujo del agua es de 6 L/s, determinar la diferencia de presión y la diferencia de altura en los tubos verticales.

Solución 

Partiendo de la ecuación del caudal, cuyo valor es Q = 6 L/s:

Q = A·v

Se tiene entonces que la velocidad en tramo ancho es 1,5 m/s y en el tramo estrecho 6 m/s.

Luego, aplicando e igualando la ecuación de Bernoulli sobre el tramo ancho y el estrecho, se obtiene una diferencia de presión de 1700 Pa, que corresponde a una diferencia de altura en los tubos verticales de 1,72 metros.