Velocidad areolar: cómo se calcula y ejercicios resueltos
La velocidad areolar es el área barrida por unidad de tiempo y es constante. Es propia de cada planeta y surge a partir de la descripción de la segunda ley de Kepler en forma matemática. En este artículo te explicaremos en qué consiste y cómo se calcula.
El boom que representa el descubrimiento de planetas fuera del sistema solar ha reactivado el interés en el movimiento planetario. Nada hace creer que estos exo-planetas sigan leyes distintas a las ya conocidas y válidas del sistema solar: las leyes de Kepler.
Johannes Kepler fue el astrónomo que sin la ayuda del telescopio y utilizando las observaciones de su mentor Tycho Brahe, creó un modelo matemático que describe el movimiento de los planetas alrededor del Sol.
Dejó plasmado este modelo en las tres leyes que llevan su nombre y que siguen siendo tan vigentes el día de hoy como en 1609, cuando estableció las dos primeras y en 1618, fecha en que enunció la tercera.
Índice del artículo
- 1 Leyes de Kepler
- 2 ¿Por qué los planetas se mueven elípticamente alrededor del Sol?
- 3 La magnitud de la velocidad lineal de un planeta no es constante
- 4 La velocidad areolar
- 5 Calculando la velocidad lineal y la velocidad areolar
- 6 Bibliografía
En lenguaje actual, las tres leyes de Kepler dicen así:
1. Las órbitas de todos los planetas son elípticas y el Sol está en un foco.
2. El vector de posición que va desde el Sol a un planeta barre áreas iguales en tiempos iguales.
3. El cuadrado del período orbital de un planeta es proporcional al cubo del semi-ieje mayor de la elipse descrita.
Un planeta tendrá una velocidad lineal, al igual que cualquier objeto conocido que se mueva. Y aún hay más: al escribir la segunda ley de Kepler en forma matemática, surge un nuevo concepto llamado velocidad areolar, propia de cada planeta.
La Tierra y los demás planetas se mueven alrededor del Sol gracias a que este ejerce una fuerza sobre ellos: la atracción gravitatoria. Lo mismo sucede con cualquier otra estrella y los planetas que conformen su sistema, si los tiene.
Esta es una fuerza del tipo conocido como fuerza central. El peso es una fuerza central con la que todos están familiarizados. El objeto que ejerce la fuerza central, sea el Sol o una estrella lejana, atrae a los planetas hacia su centro y estos se mueven describiendo una curva cerrada.
En principio esta curva se puede aproximar como una circunferencia, tal como lo hizo Nicolás Copérnico, astrónomo polaco creador de la teoría heliocéntrica.
La fuerza responsable es la atracción gravitatoria. Esta fuerza depende directamente de las masas de la estrella y el planeta en cuestión y es inversamente proporcional al cuadrado de la distancia que los separa.
El problema no es tan fácil, pues en un sistema solar, todos los elementos interactúan de esta manera, añadiendo complejidad al asunto. Además no son partículas, pues estrellas y planetas tienen tamaño mensurable.
Por esta razón, el punto central de la órbita o circuito recorrido por los planetas no está exactamente centrado en la estrella, sino en un punto conocido como el centro de gravedad del sistema sol-planeta.
La órbita resultante es elíptica. La siguiente imagen lo muestra, tomando como ejemplo la Tierra y el Sol:
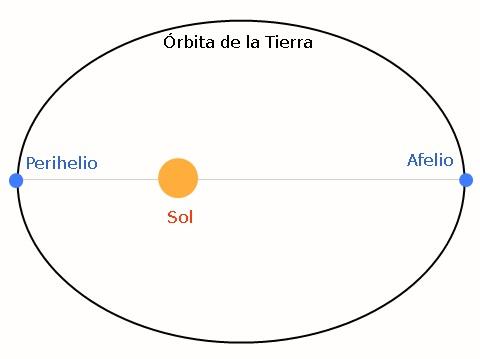
El afelio es la posición más lejana de la Tierra al Sol, mientras que el perihelio es el punto más cercano. La elipse puede ser más o menos achatada, según las características del sistema estrella – planeta.
Los valores de afelio y perihelio varían anualmente, ya que los demás planetas causan perturbaciones. Para otros planetas, estas posiciones se denominan apoastro y periastro respectivamente.
Kepler descubrió que cuando un planeta orbita alrededor del Sol, durante su movimiento barre áreas iguales en tiempos iguales. La figura 2 muestra gráficamente el significado de esto:
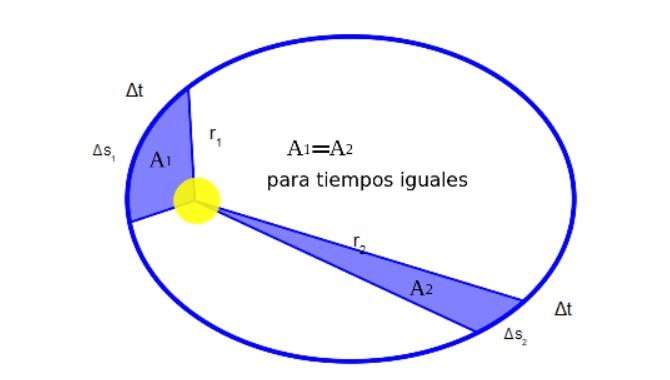
Matemáticamente, el hecho de que A1 sea igual a A2 se expresa así:
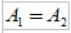
Los arcos recorridos Δs son pequeños, de manera que cada área puede aproximarse a la de un triángulo:
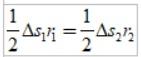
Como Δs=vΔt, donde v es la velocidad lineal del planeta en un punto dado, al sustituir tenemos:
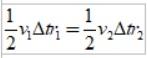
Y puesto que el intervalo de tiempo Δt es el mismo, se obtiene:
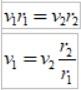
Como r2 > r1, entonces v1 > v2, en otras palabras, la velocidad lineal de un planeta no es constante. De hecho la Tierra va más deprisa cuando está en el perihelio que cuando está en el afelio.
Por lo tanto la velocidad lineal de la Tierra o de cualquier planeta alrededor del Sol no es una magnitud que sirva para caracterizar el movimiento de dicho planeta.
La segunda ley de Kepler sugiere una nueva magnitud llamada velocidad areolar. Se define como el área barrida por unidad de tiempo y es constante. Para calcularla se utiliza la siguiente figura:
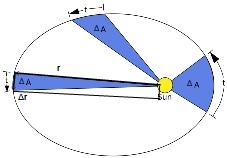
Se escoge una pequeña área barrida por la Tierra mientras realiza su circuito elíptico, la cual denotaremos como ΔA. El tiempo necesario para ello es Δt.
En la figura 3 se muestra el vector de posición de la Tierra respecto al Sol, denotado por r. Cuando la Tierra se mueve, experimenta un desplazamiento Δr.
Esta área corresponde a la mitad del área del rectángulo mostrado en la figura 3:
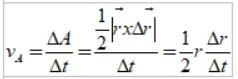
El cociente Δr/Δt es precisamente la velocidad lineal de la Tierra, entonces la velocidad areolar queda como:
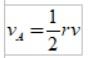
Las unidades de vA en el Sistema Internacional son:
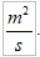
Nótese que si bien tanto r como v varían, el producto permanece constante. Ello convierte a la velocidad areolar en una magnitud muy adecuada para caracterizar el movimiento de un planeta alrededor de su estrella.
El producto de r y v es la magnitud del momento angular L, de manera que la velocidad areolar puede expresarse como:
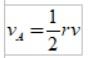
Con el siguiente ejemplo pondremos de manifiesto como calcular la velocidad areolar cuando se conocen algunos parámetros del movimiento planetario:
Un exo-planeta se mueve alrededor de su sol siguiendo una órbita elíptica, de acuerdo a las leyes de Kepler. Cuando está en el periastro, su radio vector es r1 = 4·107 km, y cuando está en el apoastro es r2 = 15·107 km. La velocidad lineal en su periastro es v1 = 1000 km/s.
Calcular:
A) La magnitud de la velocidad en el apoastro.
B) La velocidad areolar del exo-planeta.
C) La longitud del semieje mayor de la elipse.
Respuesta A)
Se utiliza la ecuación:
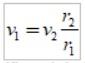
en la cual se sustituyen los valores numéricos.
Cada término se identifica del siguiente modo:
v1 = velocidad en apoastro; v2 = velocidad en el periastro;r1= distancia del apoastro,
r2= distancia del periastro.
Con estos valores se obtiene:

Respuesta B)
La ecuación a utilizar es
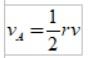
en la cual puede sustituirse la pareja de valores r y v del periastro o del apoastro, puesto que vA es una constante del planeta:

Respuesta C)
La longitud del semieje mayor de la elipse es la semisuma del apoastro y el periastro:
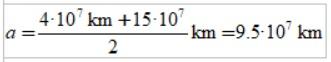
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. México. Cengage Learning Editores. 367-372.
- Stern, D. (2005). Las Tres Leyes de Kepler del Movimiento Planetario. Recuperado de pwg.gsfc.nasa.gov
- Nota: el ejercicio propuesto fue tomado y modificado del siguiente texto de un libro de McGrawHill. Lamentablemente se trata de un capítulo aislado en formato pdf, sin el título ni el autor: mheducation.es/bcv/guide/capitulo/844817027X.pdf
