Densidad aparente: fórmula, unidades y ejercicios resueltos
La densidad aparente de una muestra se define como el cociente entre su masa y el volumen sin alterar, que incluye todos los espacios o poros que contenga. Si en estos espacios hay aire, la densidad aparente ρb, o bulk density es:
ρb = Masa / Volumen = Masa partículas + Masa aire /Volumen partículas+ Volumen aire

Cuando se calcula la densidad aparente de una muestra de suelo, hay que secarla previamente en un horno a 105 ºC hasta que la masa sea constante, indicativo de que todo el aire se ha evaporado.
De acuerdo a esta definición, la densidad aparente de los suelos o densidad seca, se calcula de esta forma:
ρs = Peso de los elementos sólidos / Volumen sólidos + Volumen poros
Denotando como Ms al peso o masa secos y Vt = Vs + Vp como el volumen total, la fórmula queda:
ρs = Ms / Vt
Índice del artículo
- 1 Unidades
- 2 Densidad aparente del suelo
- 3 ¿Cómo medir la densidad aparente?
- 4 Ejercicio resuelto
- 5 Referencias
Las unidades de la densidad aparente en el Sistema Internacional de Unidades son kg/m3. Sin embargo, otras unidades como g/cm3 y megagramos/metro cúbico: Mg/m3 también se utilizan ampliamente.
El concepto de densidad aparente es muy útil cuando se trata de materiales heterogéneos y porosos como los suelos, pues es indicativo de su capacidad de drenaje y aireación, entre otras cualidades.
Por ejemplo, los suelos poco porosos tienen densidades aparentes elevadas, son compactos y tienden a anegarse fácilmente, a diferencia de los suelos porosos.
Cuando en los poros de la muestra hay agua u otro fluido, el volumen después de secado disminuye, por lo tanto al momento de efectuar los cálculos es preciso conocer la proporción de agua original (ver ejemplo resuelto).
La densidad aparente de los materiales en general, incluido el suelo, es muy variable, ya que hay factores como el grado de compactación, la presencia de materia orgánica, su textura, estructura, la profundidad y otros más, que afectan la forma y la cantidad de los espacios porosos.
Los suelos se definen como una mezcla heterogénea de sustancias inorgánicas, sustancias orgánicas, aire y agua. Al tacto pueden ser de textura fina, mediana o gruesa, mientras que las partículas componentes pueden organizarse de diversas maneras, un parámetro que se conoce como estructura.
Los suelos finos, bien estructurados y con alto porcentaje de materia orgánica suelen tener valores bajos de densidad aparente. Por el contrario, los suelos gruesos, con menor cantidad de materia orgánica y poca estructuración, tienden a tener valores más altos.
De acuerdo a su textura la densidad aparente tiene los siguientes valores:
| Textura | Densidad Aparente (g/cm3) |
|---|---|
| Fina | 1.00 – 1.30 |
| Mediana | 1.30 – 1.50 |
| Gruesa | 1.50 – 1.70 |
Estos valores sirven como referencia general. En suelos turbosos, abundantes en residuos vegetales, la densidad aparente puede ser tan baja como 0.25 g/cm3, si se trata de un suelo mineral volcánico está alrededor de 0.85 g/cm3, mientras que en suelos muy compactados alcanza 1.90 g/cm3.
El valor de densidad aparente también aumenta con la profundidad, ya que el suelo por lo general está más compactado y tiene un porcentaje menor de materia orgánica.
El interior del terreno está compuesto de capas o estratos horizontales, denominadas horizontes. Los horizontes tienen diferentes texturas, composición y compactación. Por lo tanto presentan variación en cuanto a la densidad aparente.
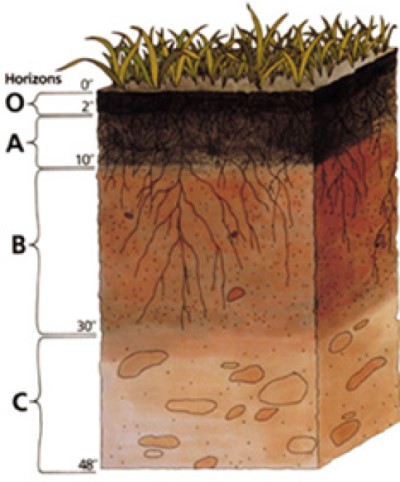
Un estudio del suelo se basa en su perfil, el cual consta de diversos horizontes que se suceden ordenadamente en forma vertical.
Puesto que la variabilidad en la densidad aparente es muy grande, con frecuencia hay que medirla directamente mediante diversos procedimientos.
El método más simple consiste en extraer del suelo una muestra, introduciendo en él una barrena con un cilindro metálico espacial de volumen conocido y asegurándose de no compactar el suelo. La muestra extraída queda sellada, para evitar la pérdida de humedad o la alteración de las características.
Luego en el laboratorio la muestra se extrae, se pesa y después se coloca en un horno a 105 º C para que se seque durante 24 horas.
Si bien es la manera más simple de encontrar la densidad seca del suelo, no es el más recomendable para suelos con texturas muy sueltas o llenos de piedras.
Para estos es preferible el método de cavar un hoyo y guardar la tierra extraída, que será la muestra para secar. El volumen de la muestra se determina vertiendo arena seca o agua en el hoyo cavado.
En todo caso, a partir de la muestra es posible determinar propiedades muy interesantes del suelo para caracterizarlo. El siguiente ejercicio resuelto nos describe cómo hacerlo.
Una muestra de arcilla de longitud 100 mm se extrae del cilindro de muestra, cuyo diámetro interno también es de 100 mm. Al pesarla se obtiene una masa de 1531 g, que una vez seca se reduce a 1178 g. La gravedad específica de las partículas es 2.75. Se pide calcular:
a) La densidad aparente de la muestra
b) El contenido de humedad
c) La relación de vacíos
d) La densidad seca
e) El grado de saturación
f) El contenido de aire
El volumen sin alterar Vt es el volumen original de la muestra. Para un cilindro de diámetro D y altura h, el volumen es:
V cilindro = Vt = Área de la base x altura = πD2/4 = π x (100 x 10-3 m)2 x 100 x 10 -3 m/ 4 = 0.000785 m3
El enunciado afirma que la masa de la muestra es Ms = 1531 g, por lo tanto según la ecuación dada al comienzo:
ρb = Ms / Vt = 1531 g / 0.000785 m3 = 1950319 g/ m3 = 1.95 Mg/m3
Como tenemos la masa original y la masa seca, la masa del agua contenida en la muestra es la diferencia de estas dos:
M agua = 1531 g – 1178 g = 353 g
El porcentaje de humedad en la muestra se calcula así:
% Humedad = (Masa agua / Ms ) x 100 % = (353 g / 1178 g) = 29. 97 %
Para hallar la relación de vacíos es preciso desglosar el volumen total de la muestra Vt en:
V t = V partículas + Volumen poros
El volumen ocupado por las partículas se obtiene de la masa seca y la gravedad específica, datos que se obtienen del enunciado. La gravedad específica sg es el cociente entre la densidad del material y la densidad del agua en condiciones estándar, por lo tanto la densidad del material es:
ρ = sg x ρagua = 2.75 x 1 g/cm3 = 2.75 g/cm3
ρ = Ms / Vs → Vs = 1.178 g / 2.75 g/cm3 = 0.428 cm3 = 0.000428 m3
El volumen de vacíos en la muestra es Vv = Vt – Vs = 0.000785 m3 – 0.000428 m3 = 0.000357 m3.
La relación de vacíos e es:
e = Vv /Vs = 0.000357 m3 / 0.000428 m3 = 0.83
La densidad seca de la muestra se calcula como se indicó en la introducción:
ρs = Peso de los elementos sólidos / Volumen sólidos + Volumen poros= 1178 g/0.000785 m3 = 1.5 Mg/m3
El grado de saturación es S = (Vagua / Vv ) x 100%. Puesto que conocemos la masa de agua en la muestra, calculada en el ítem b) y la densidad de la misma, el cálculo su volumen es inmediato:
ρagua = Magua / V agua → Vagua = 353 g / 1 g/cm3 = 353 cm3 = 0.000353 m3
Por otro lado el volumen de vacíos se calculó en el ítem c)
S = (0.000353 m3 / 0.000357 m3) x 100% = 98.9%
Finalmente el contenido porcentual de aire es A = (Vaire / Vt) x 100%. El volumen de aire corresponde a:
Vv – Vagua = 0.000357 m3 – 0.000353 m3 = 0.000004 m3
A = (Vaire / Vt) x 100% = (0.000004 m3/ 0.000785 m3) x100 % = 0.51 %
- Berry, P. Mecánica de Suelos. McGraw Hill.
- Construmática. Densidad Aparente. Recuperado de: construmatica.com.
- NRCS. Soil Bulk Density. Recuperado de: nrcs.usda.gov.
- UNAM. Departamento de Edafología. Manual de procedimientos analíticos de Física de Suelos. Recuperado de: geologia.unam.mx.
- Wikipedia. Bulk Density. Recuperado de: en.wikipedia.org.
- Wikipedia. Suelo. Recuperado de: en.wikipedia.org.
