¿Qué es el módulo de corte, rigidez o cizalladura? (Ejercicios resueltos)
El módulo de corte describe la respuesta de un material ante la aplicación de un esfuerzo cortante que lo deforma. Otras denominaciones de uso frecuente para el módulo de corte son módulo de cizalla, cizalladura, de elasticidad transversal o de elasticidad tangencial.
Cuando los esfuerzos son pequeños, las deformaciones son proporcionales a ellos, de acuerdo a la ley de Hooke, siendo el módulo de corte la constante de proporcionalidad. Por lo tanto:
Módulo de corte = Esfuerzo de corte/Deformación
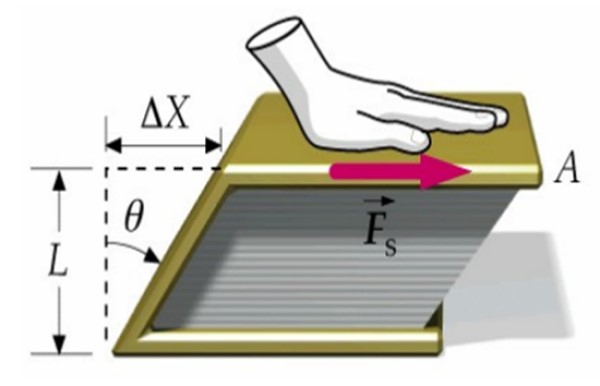
Supongamos que se aplica una fuerza sobre la tapa de un libro, estando la otra fija sobre la superficie de la mesa. De esta forma, el libro como un todo no se desplaza, sino que se deforma al moverse la tapa superior respecto a la inferior en la cantidad Δx.
El libro pasa de tener una sección trasversal rectangular a una sección en forma de paralelogramo, tal como vemos en la imagen superior.
Sea:
τ = F/A
El esfuerzo o tensión de corte, siendo F la magnitud de la fuerza aplicada y A el área sobre la cual actúa.
La deformación causada viene dada por el cociente:
δ = Δx / L
Por lo tanto el módulo de corte, al que denotaremos como G, es:
Y como Δx / L carece de dimensiones, las unidades de G son las mismas que las del esfuerzo de corte, el cual es la razón entre la fuerza y el área.
En el Sistema Internacional de Unidades, dichas unidades son Newton/metro cuadrado o pascal, abreviado Pa. Y en unidades anglosajonas es libra /pulgada cuadrada, abreviado psi.
Índice del artículo
Bajo la acción de fuerzas cortantes como las descritas, los objetos ofrecen una resistencia parecida a la del libro, en el cual las capas interiores deslizan. Este tipo de deformación solamente puede darse en cuerpos sólidos, que tienen rigidez suficiente como para oponerse a ser deformados.
En cambio, los líquidos no ofrecen esta clase de resistencia, pero sí pueden experimentar deformaciones de volumen.

A continuación se tiene el módulo de corte G en Pa para diversos materiales empleados con frecuencia en construcción y en la fabricación de maquinarias y repuestos de todo tipo:
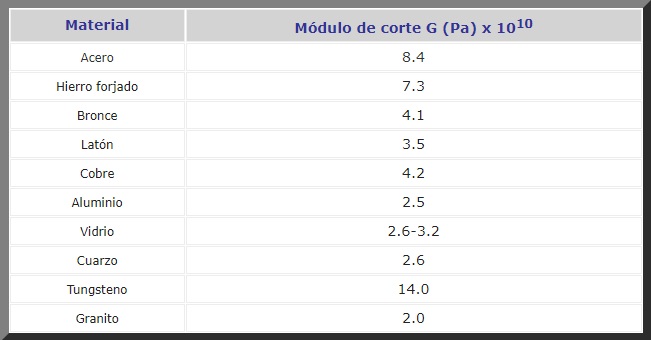
Para encontrar el valor del módulo de corte, hay que someter a prueba muestras de cada material y examinar su respuesta ante la aplicación de un esfuerzo de corte.
La muestra es una varilla hecha con el material, con radio R y longitud L conocidos, la cual está fija en un extremo, mientras que el otro se conecta al eje de una polea libre de girar.
La polea tiene atada una cuerda, en cuyo extremo libre va colgada una pesa que ejerce una fuerza F sobre la varilla a través de la cuerda. Y esta fuerza a su vez produce un momento M en la varilla, que entonces gira un pequeño ángulo θ.
Un esquema del montaje se puede ver en la siguiente figura:
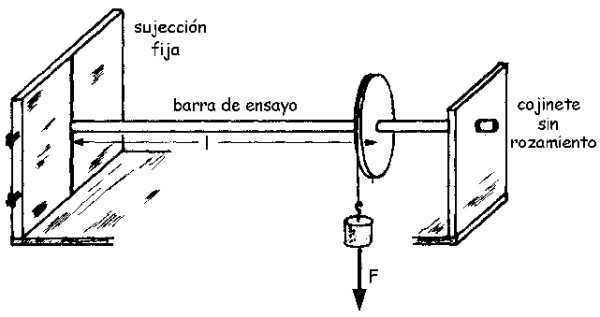
La magnitud del momento M, la cual denotamos como M (sin negrita) está relacionada con el ángulo girado θ a través del módulo de corte G de acuerdo a la ecuación siguiente (se deduce mediante una integral sencilla):
Como la magnitud del momento es igual al producto del módulo de la fuerza F por el radio de la polea Rp:
M =F.Rp
Y la fuerza es el peso que cuelga W, entonces:
M = W.Rp
Sustituyendo en la ecuación de la magnitud del momento:
Se tiene la relación entre peso y ángulo:
Esta relación entre las variables W y θ es lineal, así que se miden los distintos ángulos producidos colgando diferentes pesas.
Las parejas de peso y ángulo se grafican sobre un papel milimetrado, se ajusta la mejor recta que pasa por los puntos experimentales y se calcula la pendiente m de dicha recta.
Una varilla de 2.5 metros de largo y radio 4.5 mm está fija en un extremo. El otro se conecta a una polea de radio 75 cm que tiene colgando un peso W de 1.3 kg. El ángulo girado es de 9.5º.
Con estos datos se pide calcular el módulo de corte G de la varilla.
Solución
De la ecuación:
Se despeja G:
Y se sustituyen los valores dados en el enunciado, teniendo cuidado de expresar todos los datos en el Sistema Internacional de Unidades SI:
R = 4.5 mm = 4.5 x 10 -3 m
Rp = 75 cm = 0.075
Para pasar de kilogramos (que en realidad son kilogramos – fuerza) a newton se multiplica por 9.8:
W = 1.3 kg-fuerza = 1.3 x 9.8 N = 12.74 N
Y por último, los grados deben estar en radianes:
9.5 º = 9.5 x2π /360 radianes = 0.1658 radianes.
Con todo esto se tiene:
= 2.237 x 1010 Pa
Un cubo hecho de gel tiene 30 cm de lado. Una de sus caras está fija, pero al mismo tiempo, a la cara opuesta se le aplica una fuerza paralela de 1 N, que gracias a ello se desplaza 1 cm (véase el ejemplo del libro en la figura 1).
Se pide calcular con estos datos:
a) La magnitud del esfuerzo cortante
b) La deformación unitaria δ
c) El valor del módulo de corte
Solución a
La magnitud del esfuerzo cortante es:
τ = F/A
Con:
A = lado2 = (30 x 10-2 cm)2 = 0.09 m2
Por lo tanto:
τ = 1 N / 0.09 m2 = 11.1 Pa
Solución b
La deformación unitaria no es otra que el valor de δ, dado por :
δ = Δx / L
El desplazamiento de la cara sometida a la fuerza es de 1 cm, luego:
δ =1 / 30 = 0.0333
Solución c
El módulo de corte e el cociente entre el esfuerzo de corte y la deformación unitaria:
G = Esfuerzo de corte/Deformación
Por lo tanto:
G = 11.1 Pa / 0.033 = 336.4 Pa
- Beer, F. 2010. Mecánica de materiales. McGraw Hill. 5ta. Edición.
- Franco García, A. Sólido Rígido. Medida del módulo de cizallamiento. Recuperado de: sc.ehu.es.
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
- Resnick, R. (1999). Física. Vol. 1. 3ra Ed. en español. Compañía Editorial Continental S.A. de C.V.
- Universidad de Valladolid. Departamento de Física de la Materia Condensada. Selección de problemas. Recuperado de: www4.uva.es.
