Efecto Joule: explicación, ejemplos, ejercicios, aplicaciones
El efecto Joule o ley de Joule es el resultado de la transformación de la energía eléctrica en calor, que tiene lugar cuando una corriente eléctrica atraviesa un conductor. Este efecto está presente siempre que se enciende cualquier aparato o dispositivo que necesite electricidad para funcionar.

Otras veces es indeseable y se busca minimizarlo, por eso a la PC de escritorio se le añaden ventiladores para disipar el calor, ya que puede causar fallos a los componentes internos.
Los aparatos que se valen del efecto Joule para producir calor, tienen en su interior una resistencia que se calienta cuando se le hace pasar corriente, llamada elemento de calefacción.
Índice del artículo
El efecto Joule tiene su origen a escala microscópica en las partículas, tanto las que conforman un material como las que transportan la carga eléctrica.
Los átomos y las moléculas en una sustancia se encuentran en su posición más estable en el interior de esta. Por su parte, la corriente eléctrica consiste en un movimiento ordenado de cargas eléctricas, que provienen del polo positivo de la batería. Al salir de allí tienen mucha energía potencial.
A su paso, las partículas cargadas impactan a las del material y las ponen a vibrar. Estas tratarán de recobrar el equilibrio que tenían previamente, entregando el exceso de energía a su entorno en forma de calor perceptible.
La cantidad de calor Q desprendido depende de la intensidad de la corriente I, el tiempo por el que circula dentro del conductor Δt y del elemento resistivo R:
Q = I2.R. Δt (joules)
La ecuación anterior recibe el nombre de ley de Joule-Lenz.
Dos físicos, el británico James Joule (1818-1889) y el ruso Heinrich Lenz (1804-1865) observaron, de manera independiente, que un alambre que transportaba corriente no solamente se calentaba, sino que su corriente iba disminuyendo durante el proceso.
Luego se estableció que, la cantidad de calor disipada por la resistencia es proporcional a:
– El cuadrado de la intensidad de la corriente circulante.
– El tiempo que permanecía dicho corriente fluyendo por el conductor.
– La resistencia de dicho conductor.
Las unidades del calor son las mismas unidades de la energía: los joules, abreviados como J. El joule es una unidad de energía bastante pequeña, entonces suelen emplearse otras como las calorías, por ejemplo.
Para transformar joules a calorías basta con multiplicar por el factor 0,24, de manera que la ecuación dada al comienzo, se expresa directamente en calorías:
Q = 0,24. I2.R. Δt (calorías)
El efecto Joule es bienvenido para producir calor localizado, como hornillas y secadores de cabello. Pero en otros casos, tiene efectos indeseados, como por ejemplo:
– Un calentamiento muy grande en los conductores puede ser peligroso, causando incendios y quemaduras.
– Los dispositivos electrónicos con transistores disminuyen su rendimiento y pueden fallar incluso si se calientan demasiado.
– Los alambres que transportan energía eléctrica experimentan siempre un calentamiento, aunque sea leve, el cual conduce a pérdidas notables de energía.
Eso se debe a que los cables que transportan corriente desde las centrales eléctricas tienen recorridos de centenares de kilómetros. Entonces buena parte de la energía que llevan no alcanza a llegar a su destino, porque se desperdicia en el camino.
Para evitarlo, se busca que los conductores tengan la menor resistencia posible. En esto influyen tres factores importantes: la longitud del alambre, el área de sección transversal y el material con que está hecho.
Los mejores conductores son los metales, siendo oro, plata, platino o cobre algunos de los más eficientes. Los alambres de los cables están hechos a base de filamentos de cobre, metal que, aunque no conduce tan bien como el oro, sí es bastante más barato.
Cuanto más largo sea un alambre, mayor resistencia tendrá, pero al fabricarlos más gruesos, la resistencia disminuye, porque esto facilita el movimiento de los portadores de carga.
Otra cosa que puede hacerse es disminuir la intensidad de la corriente, para que el calentamiento se minimice. Los transformadores se encargan de controlar la intensidad apropiadamente, por eso son tan importantes en la transmisión de energía eléctrica.
Un radiador indica que posee una potencia de 2000W y está conectado a la toma de 220 V. Calcular lo siguiente:
a) Intensidad de la corriente que circula por el radiador
b) Cantidad de energía eléctrica que se ha transformado al cabo de media hora
c) Si toda esta energía se invierte en calentar 20 litros de agua que inicialmente están a 4 ºC, ¿cuál será la máxima temperatura a la que se puede calentar el agua?
Dato: el calor específico del agua es Ce = 4180 J/kg.K
Solución a
La potencia se define como energía por unidad de tiempo. Si en la ecuación dada al comienzo pasamos el factor Δt a la derecha, se tendrá precisamente energía por unidad de tiempo:
Q = I2.R. Δt → P = Q/ Δt = I2. R
La resistencia del elemento calefactor se puede conocer a través de la ley de Ohm: V = I.R, de la cual se deduce que I = V/R. por lo tanto:
P = I2. (V/I) = I. V
Así la corriente resulta:
I = P/ V = 2000 W / 220 V = 9.09 A.
Solución b
En este caso Δt = 30 minutos = = 30 x 60 segundos =1800 segundos. También se requiere el valor de la resistencia, que se despeja de la ley de Ohm:
R = V/ I = 220 V / 9.09 A = 24.2 ohm
Se sustituyen los valores en la ley de Joule:
Q = (9.09 A)2. 24.2 ohm . 1800 s = 3.600.000 J = 3600 kJ.
Solución c
La cantidad de calor Q necesaria para elevar una cantidad de agua a cierta temperatura depende del calor específico y de la variación de temperatura que se necesita obtener. Se calcula mediante:
Q = m. Ce. ΔT
Aquí m es la masa de agua, Cees el calor específico, que ya se tiene como dato del problema y ΔT es la variación de temperatura.
La masa de agua es la que hay en 20 L. Se calcula con ayuda de la densidad. La densidad del agua ρagua es el cociente entre la masa y el volumen. Además hay que convertir los litros a metros cúbicos:
20 L = 0.02 m3
Como m = densidad x volumen = ρV, la masa es.
m = 1000 kg/m3 x 0.02 m3 = 20 kg.
ΔT= temperatura final – temperatura inicial = Tf – 4 ºC = Tf – 277.15 K
Nótese que hay que pasar de grados centígrados a kelvin, sumando 273.15 K. Sustituyendo lo anterior en la ecuación del calor:
3.600.000 J = 20 kg x 4180 J/kg . K . (Tf – 277.15)
Tf = 3.600.000 J/(20 kg x 4180 J/kg . K) + 277.15 K= 320. 2 K = 47.05 ºC.
a) Encontrar expresiones para potencia y la potencia media para una resistencia conectada a un voltaje alterno.
b) Suponga que tiene un secador de cabello con 1000W de potencia conectado a la toma de 120 V, encuentre la resistencia del elemento calefactor y la corriente pico -corriente máxima- que lo atraviesa.
c) ¿Qué sucede con el secador al conectarlo a una toma de 240 V?
Solución a
El voltaje de la toma es alterno, de la forma V = Vo. sen ωt. Por ser variable en el tiempo, es muy importante definir los valores eficaces, tanto del voltaje como de la corriente, los cuales se denotan con el subíndice “rms”, siglas de root mean square.
Estos valores para la corriente y el voltaje son:
Irms = 0.707 Io
Vrms = 0.707 Vo
Al aplicar la ley de Ohm, la corriente en función del tiempo queda como:
I = V/R = Vo. sen ωt /R = Io. sen ωt
En tal caso, la potencia en una resistencia atravesada por una corriente alterna es:
P = I2.R = (Io. sen ωt)2.R=Io2.R . sen2 ωt
Se ve que la potencia también varía con el tiempo, y que es una cantidad positiva, ya que todo está elevado al cuadrado y R siempre es > 0. El valor medio de esta función se calcula mediante integración en un ciclo y resulta:
Pmedia = ½. Io2.R = Irms2.R
En términos del voltaje y la corriente eficaces, la potencia queda así:
Pmedia = Vrms. Irms
Irms = Pmedia / Vrms = Pmedia / 0.707 Vo
Solución b
Aplicando la última ecuación con los datos suministrados:
Pmedia = 1000 W y Vrms = 120 V
Irms = Pmedia / Vrms = 1000 W / 120 V = 8.33 A
Por lo tanto la corriente máxima a través del elemento calefactor es:
Io= Irms /0.707 = 8.33 A/0.707= 11.8 A
La resistencia puede despejarse de la ecuación de la potencia media:
Pmedia = Irms2.R → R = Pmedia / Irms2 = 1000 W / (8.33 A)2 = 14.41 ohm.
Solución c
En caso de conectar a una toma de 240 V, la potencia media cambia:
Irms = Vrms / R = 240 V / 14.41 ohm =16.7 A
Pmedia = Vrms. Irms = 240 V x 16.7 A ≈ 4000 W
Esto es aproximadamente 4 veces la potencia para la que está diseñado el elemento calefactor, que se quemará en breve luego de ser conectado a esta toma.
Una bombilla incandescente produce luz y también calor, cosa que podemos notar inmediatamente al conectarla. El elemento que produce ambos efectos es un filamento de conductor muy delgado, que por ello tiene una resistencia elevada.
Gracias a este aumento de la resistencia, si bien la corriente ha disminuido en el filamento, el efecto Joule se concentra a tal punto que se produce la incandescencia. El filamento, fabricado de tungsteno debido a que tiene un alto punto de fusión de 3400 ºC, emite luz y también calor.
El dispositivo debe encerrarse en un recipiente de vidrio transparente, que se llena de un gas inerte, como argón o nitrógeno a baja presión, para evitar el deterioro del filamento. Si no se hace de esta forma, el oxígeno del aire consume el filamento y la bombilla deja de funcionar en el acto.
Los efectos magnéticos de los imanes desaparecen a altas temperaturas. Esto puede aprovecharse para crear un dispositivo que interrumpa el paso de corriente, cuando este sea excesivo. En esto consiste un interruptor magnetotérmico.
Una parte del circuito por la que circula la corriente está cerrada mediante un imán sujeto a un muelle. El imán se pega al circuito gracias a la atracción magnética y así permanece, mientras esta no se debilite por causa del calentamiento.
Cuando la corriente sobrepasa cierto valor, el magnetismo se debilita y el muelle despega el imán, haciendo que el circuito se abra. Y como la corriente necesita que el circuito esté cerrado para poder fluir, este se abre y el paso de corriente se interrumpe. De esta forma se impide el calentamiento de los cables que podría originar accidentes como incendios.
Otra forma de proteger un circuito e interrumpir oportunamente el paso de corriente es mediante un fusible, una tira de metal que cuando se calienta por efecto Joule, se derrite, dejando abierto el circuito e interrumpiendo la corriente.

Consiste en hacer pasar una corriente eléctrica por los alimentos, que naturalmente poseen resistencia eléctrica. Para ello se utilizan electrodos hechos de material anticorrosivo. La temperatura de los alimentos aumenta y el calor destruye las bacterias, ayudando a preservarlos por más tiempo.
La ventaja que presenta este método es que el calentamiento se produce en mucho menos tiempo que el que se requiere mediante técnicas convencionales. El calentamiento prolongado destruye las bacterias pero también neutraliza vitaminas y minerales que son imprescindibles.
El calentamiento óhmico, que dura apenas unos segundos, ayuda a preservar el contenido nutricional de los alimentos.
El siguiente experimento consiste en medir la cantidad de energía eléctrica convertida en energía térmica, midiendo la cantidad de calor absorbido por una masa conocida de agua. Para ello se sumerge en agua una bobina calefactora, a través de la cual se hace pasar una corriente.
– 1 vaso de poliestireno
– Multímetro
– Termómetro Celsius
– 1 fuente de poder ajustable, de rango 0-12 V
– Balanza
– Cables de conexión
– Cronómetro
La bobina se calienta por efecto joule y, por lo tanto, el agua también. Hay que medir la masa de agua y su temperatura inicial, y determinar hasta que temperatura vamos a calentarla.
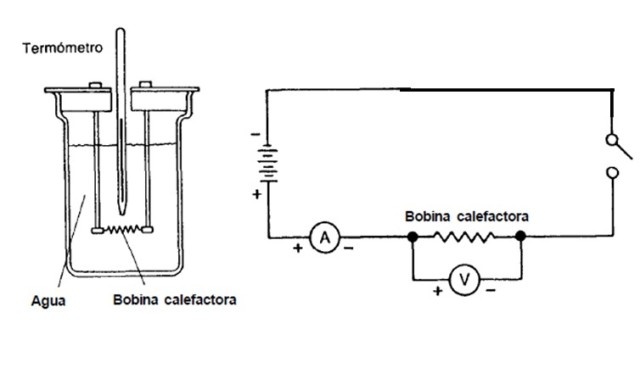
Se van tomando lecturas sucesivas cada minuto, registrando los valores de corriente y voltaje. Una vez que se dispone del registro, se calcula la energía eléctrica suministrada, mediante las ecuaciones:
Q = I2.R. Δt (Ley de Joule)
V = I.R (Ley de Ohm)
Y comparar con la cantidad de calor absorbida por la masa de agua:
Q = m. Ce. ΔT (ver ejercicio resuelto 1)
Como la energía se conserva, ambas cantidades deberían ser iguales. Sin embargo, aunque el poliestireno tiene bajo calor específico y casi no absorbe energía térmica, igualmente habrá algunas pérdidas hacia la atmósfera. También hay que tomar en cuenta el error experimental.
Las pérdidas a la atmósfera se minimizan si se calienta el agua el mismo número de grados por encima de la temperatura ambiente, al que había por debajo antes de comenzar con el experimento.
En otras palabras, si el agua estaba a 10 ºC y la temperatura ambiente era de 22 ºC, entonces hay que llevar el agua hasta 32 ºC.
- Kramer, C. 1994. Prácticas de Física. McGraw Hill. 197.
- El tamiz. Efecto Joule. Recuperado de: eltamiz.com.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 5. Electrostática. Editado por Douglas Figueroa (USB).
- Giancoli, D. 2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
- Hipertextual. Qué es el efecto Joule y por qué se ha convertido en algo trascendental para nuestras vidas. Recuperado de: hipertextual.com
- Wikipedia. Efecto Joule. Recuperado de: es.wikipedia.org.
- Wikipedia. Joule heating. Recuperado de: en. wikipedia.org.
