Presión manométrica: explicación, fórmulas, ecuaciones, ejemplos
La presión manométrica Pm es aquella que se mide en relación a una presión de referencia, que en la mayoría de los casos se escoge como la presión atmosférica Patm a nivel del mar. Se trata entonces de una presión relativa, otro término por el cual se la conoce también.
La otra manera en que suele medirse la presión es comparándola con el vacío absoluto, cuya presión siempre es nula. En tal caso se habla de la presión absoluta, a la cual denotaremos como Pa.
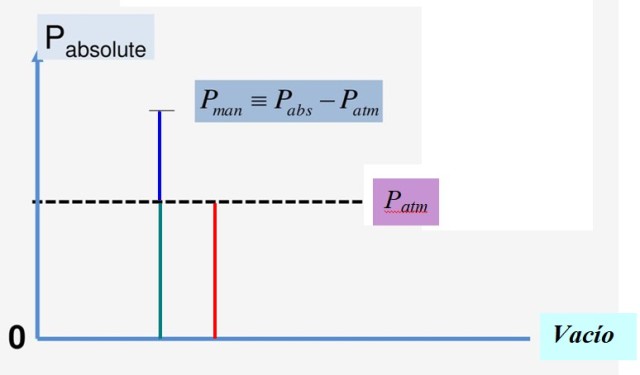
La relación matemática entre estas tres cantidades es:
Pa = Patm + Pm
Por lo tanto:
Pm = Pa – Patm
La figura 1 ilustra convenientemente esta relación. Puesto que la presión del vacío es 0, la presión absoluta siempre es positiva y lo mismo pasa con la presión atmosférica Patm.
La presión manométrica se suele utilizar para denotar presiones por encima de la presión atmosférica, como por ejemplo la que llevan los neumáticos o la que hay en el fondo del mar o de una piscina, la cual es ejercida por el peso de la columna de agua. En estos casos Pm > 0, ya que Pa > Patm.
Sin embargo, existen presiones absolutas por debajo de Patm. En estos casos Pm 0 y recibe el nombre de presión de vacío y no debe confundirse con la presión del vacío ya descrita, que es la ausencia de partículas capaces de ejercer presión.
Índice del artículo
La presión en un fluido -líquido o gas-, es una de las variables más significativas en su estudio. En un fluido estacionario, la presión es la misma en todos los puntos a una misma profundidad sin importar la orientación, mientras que el movimiento de los fluidos en las tuberías es causado por los cambios de la presión.
La presión media se define como el cociente entre la fuerza perpendicular a una superficie F⊥y el área de dicha superficie A, que se expresa matemáticamente de la siguiente manera:
P = F⊥ /A
La presión es una cantidad escalar, cuyas dimensiones son de fuerza por unidad de área. Las unidades de su medida en el Sistema Internacional de Unidades (SI) son newton/m2, llamada Pascal y abreviado como Pa, en honor a Blaise Pascal (1623-1662).
Los múltiplos como kilo (103) y mega (106) son de uso frecuente, ya que la presión atmosférica suele estar en el rango de 90.000 – 102.000 Pa, lo que es igual a: 90 – 102 kPa. No son raras las presiones del orden de los mega pascales, por eso importante familiarizarse con los prefijos.
En las unidades anglosajonas la presión se mide en libras/pie2, sin embargo, lo común es que se haga en libras/pulgada2 o psi (pounds-force per square inch).
Cuanto más nos sumergimos en el agua de una piscina o en el mar, más presión experimentamos. Por el contrario, el aumentar la altura, la presión atmosférica disminuye.
La presión atmosférica media a nivel del mar se establece en 101300 Pa o 101.3 kPa, mientras que en la fosa de las Marianas en el Pacífico Occidental –la mayor profundidad que se conoce- es unas 1000 veces mayor y en la cima del Everest es de apenas 34 kPa.
Está claro que la presión y la profundidad (o la altura) están relacionadas. Para saberlo en el caso de un fluido en reposo (equilibrio estático) se considera una porción de fluido con forma de disco, confinada en un recipiente, (ver figura 2). El disco tiene sección transversal de área A, peso dW y altura dy.
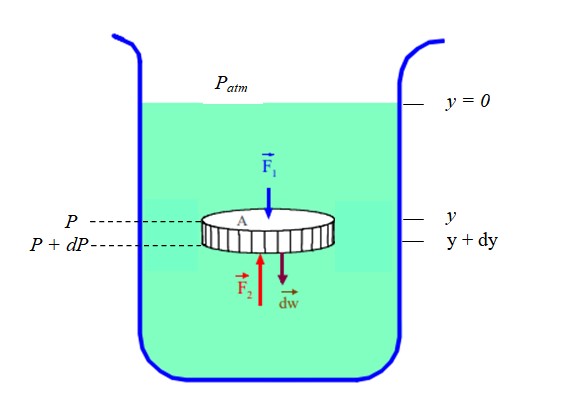
Llamaremos P a la presión que existe a profundidad “y” y P + dP a la presión que existe a profundidad (y + dy). Puesto que la densidad ρ del fluido es la razón entre su masa dm y su volumendV, se tiene que:
ρ = dm/ dV ⇒ dm= ρ.dV
Por lo tanto el peso dW del elemento es:
dW = g. dm = ρ.g.dV
Y ahora se aplica la segunda Ley de Newton:
Σ Fy = F2 – F1 – dW = 0
(P + dP).A – P.A – ρ.g.dV = 0
(P + dP).A – P.A – ρ.g. A. dy = 0
dP = ρ.g.dy
Solución de la ecuación diferencial
Integrando a ambos lados y considerando que la densidad ρ, así como la gravedad g son constantes, se encuentra la expresión buscada:
P2 – P1 =ΔP = ρ.g.(y2 – y1)
ΔP = ρ.g. Δy
Si en la expresión anterior se elige P1 como la presión atmosférica y y1 como la superficie del líquido, entonces y2 se encuentra ubicada a una profundidad h y ΔP= P2 – Patm es la presión manométrica en función de la profundidad:
Pm = ρ.g.h
En caso de necesitar el valor de la presión absoluta, simplemente se le suma la presión atmosférica al resultado anterior.
Para la medida de la presión manométrica se utiliza un dispositivo llamado manómetro, que generalmente ofrecen diferencias de presión. Al final se describirán el principio de funcionamiento de un manómetro en forma de tubo en U, pero ahora veamos algunos ejemplos y consecuencias importantes de la ecuación deducida previamente.
La ecuación ΔP = ρ.g.(y2 – y1) puede escribirse como P = Po + ρ.g.h, donde P es la presión a la profundidad h, mientras que Poes la presión en la superficie del fluido, usualmente Patm.
Evidentemente que cada vez que aumente Po, aumenta P en la misma cantidad, siempre y cuando se trate de un fluido cuya densidad sea constante. Es precisamente lo que se supuso al considerar ρ constante y colocarla fuera de la integral resuelta en el apartado anterior.
El principio de Pascal afirma que cualquier aumento en la presión de un fluido confinado en equilibrio, se transmite sin variación alguna a todos los puntos de dicho fluido. Mediante esta propiedad, es posible multiplicar la fuerza F1 aplicada al émbolo pequeño de la izquierda, y obtener F2 en el de la derecha.
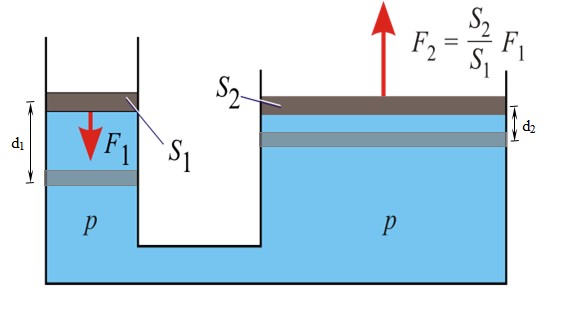
Los frenos del automóvil funcionan bajo este principio: se aplica una fuerza relativamente pequeña sobre el pedal, la cual se convierte en una fuerza mayor sobre el cilindro de freno en cada rueda, gracias al fluido utilizado en el sistema.
La paradoja hidrostática afirma que la fuerza debida a la presión de un fluido en el fondo de un recipiente puede ser igual, mayor o menor que el peso del fluido mismo. Pero al poner el recipiente encima de la báscula, esta registrará normalmente el peso del fluido (más el del recipiente claro está). ¿Cómo explicar esta paradoja?
Partimos del hecho de que la presión en el fondo del recipiente depende exclusivamente de la profundidad y es independiente de la forma, tal como se dedujo en el apartado precedente.
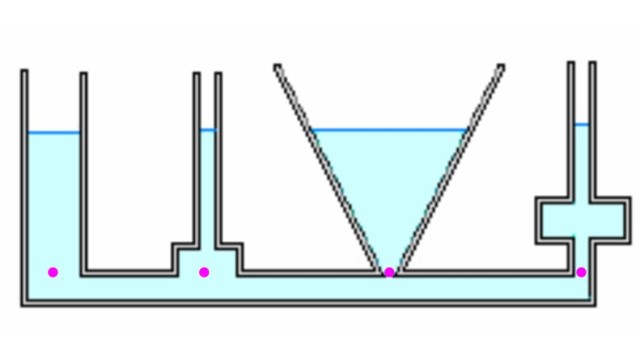
Veamos algunos recipientes diferentes. Al estar comunicados, cuando se llenan de líquido todos alcanzan la misma altura h. Los puntos destacados están a la misma presión, puesto que se encuentran a igual profundidad. Sin embargo, la fuerza debida a la presión en cada punto puede diferir del peso, (véase el ejemplo 1 a continuación).
Comparar la fuerza ejercida por la presión sobre el fondo de cada uno de los recipientes con el peso del fluido, y explique el por qué de las diferencias, si las hay.
Recipiente 1
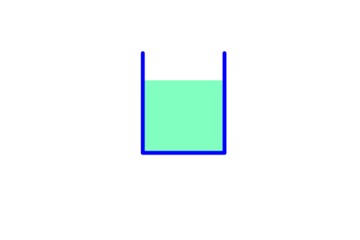
En este recipiente el área de la base es A, por lo tanto:
Peso del fluido: mg = ρ.V.g = ρ . A .h . g
Presión sobre el fondo: ρ. g. h
Fuerza debida a la presión: F = P.A = ρ. g. h. A
El peso y la fuerza debida a la presión son iguales.
Recipiente 2
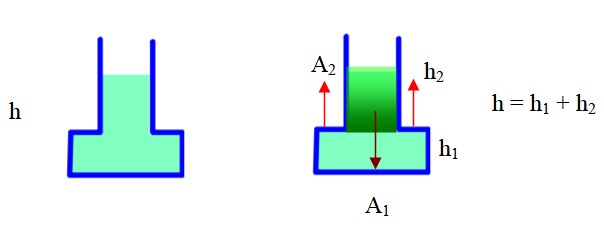
El recipiente tiene una parte estrecha y una parte ancha. En el esquema de la derecha se ha divido en dos partes y se hará uso de la geometría para encontrar el volumen total. El área A2 es externa al recipiente, h2 es la altura de la parte estrecha, h1 es la altura de la parte ancha (base).
El volumen completo es el volumen de la base + el volumen de la parte estrecha. Con estos datos se tiene:
Peso del fluido: m . g = ρ . g. V = ρ . g. [A1 .h1+ (A1 -A2) .h2]=
= ρ . g (A1.h –A2h2)= ρ . g . A1.h – ρ . g . A.. h2 (Se ha hecho uso de h= h1 +h2)
Presión sobre el fondo: P =ρ. g. h
Fuerza sobre el fondo debida a la presión: F = P. A1 =ρ. g. h. A1
Comparando el peso del fluido con la fuerza debida a la presión se advierte que esta es mayor que el peso.
Lo que sucede es que el fluido también ejerce fuerza sobre la parte del escalón en el recipiente (ver las flechas en rojo de la figura) que están incluidas en el cálculo anterior. Esta fuerza hacia arriba contrarresta a las que se ejercen hacia abajo y el peso que registra la báscula es la resultante de estas. De acuerdo a esto, la magnitud del peso es:
W = Fuerza sobre el fondo – Fuerza sobre la parte escalonada = ρ . g . A1.h – ρ . g . A.. h2
En la figura se muestra un manómetro de tubo abierto. Consiste en un tubo en U, en el cual uno de los extremos se encuentra a presión atmosférica y el otro se conecta a S, el sistema cuya presión se va a medir.
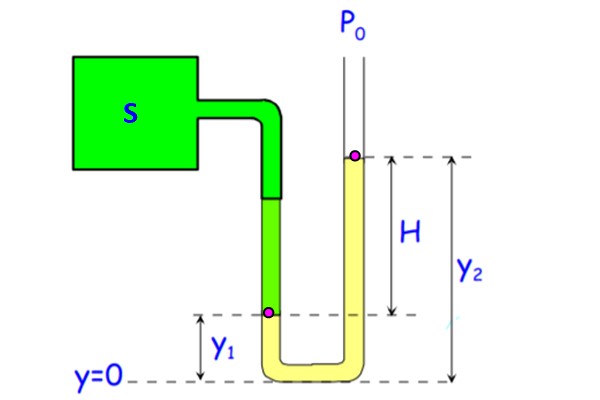
El líquido en el tubo (en amarillo en la figura) puede ser agua, aunque de preferencia se utiliza mercurio para reducir el tamaño del dispositivo. (Una diferencia de 1 atmósfera o 101.3 kPa requiere de una columna de agua de 10.3 metros, nada portátil).
Se pide encontrar la presión manométrica Pm en el sistema S, en función de la altura H de la columna de líquido.
Solución
La presión en el fondo para ambas ramas del tubo es la misma, por estar a igual profundidad. Sea PA la presión en el punto A, ubicado en y1 y PB las del punto B que se encuentra a la altura y2. Puesto que el punto B se encuentra en la interfaz de líquido y aire, la presión allí es Po. En esta rama del manómetro, la presión en el fondo es:
Po + ρ.g.y2
Por su parte, la presión en el fondo para la rama de la izquierda es:
P + ρ.g.y1
Donde P es la presión absoluta del sistema y ρ es la densidad del fluido. Igualando ambas presiones:
Po + ρ.g.y2 = P + ρ.g.y1
Despejando P:
P = Po + ρ.g.y2 – ρ.g.y1 = Po + ρ.g(y2 – y1)= Po + ρ.g. H
Por lo tanto, la presión manométrica Pm viene dada por P – Po = ρ.g. H y para tener su valor, basta con medir la altura a la que sube el líquido manométrico y multiplicarla por el valor de g y la densidad del fluido.
- Cimbala, C. 2006. Mecánica de Fluidos, Fundamentos y Aplicaciones. Mc. Graw Hill. 66-74.
- Figueroa, D. 2005. Serie: Física para Ciencias e Ingeniería. Volumen 4. Fluidos y Termodinámica. Editado por Douglas Figueroa (USB). 3-25.
- Mott, R. 2006. Mecánica de Fluidos. 4ta. Edición. Pearson Educación. 53-70.
- Shaugnessy, E. 2005. Introduction to Fluid Mechanics.Oxford University Press. 51 – 60.
- Stylianos, V. 2016. A simple explanation of the classic hydrostatic paradox. Recobrado de: haimgaifman.files.wordpress.com
