Presión relativa: fórmula, cómo se calcula, ejemplos, ejercicio
La presión relativa es la que se mide respecto a un cierto valor o datum, que por lo general es la presión atmosférica a nivel del mar (presión atmosférica estándar). Esto es apropiado debido a que gran parte de las mediciones de presión se llevan a cabo bajo las capas gaseosas que constituyen la atmósfera, las cuales ejercen su propia presión.
En cambio, la presión absoluta se mide con respecto a un vacío total, en el cual no hay moléculas interactuando. En un contenedor en el cual se ha hecho el vacío, no existen partículas actuando desde el interior sobre las paredes ni sobre objetos dentro de él.

Las presiones que se miden pueden estar por encima o por debajo de la presión atmosférica. En el primer caso se habla de la presión manométrica y en el segundo de la presión de vacío.
Normalmente las presiones que se miden cotidianamente en los neumáticos y la presión arterial, son presiones relativas, mientras que cuando se mide la presión atmosférica mediante un barómetro, se trata de una presión absoluta.
Índice del artículo
- 1 Fórmula de la presión relativa
- 2 ¿Cómo se calcula la presión relativa?
- 3 Variación de la presión con la profundidad
- 4 Ejemplos de presión relativa
- 5 Ejercicio resuelto
- 6 Referencias
Siendo la presión relativa la diferencia entre la presión absoluta Pabs y la presión atmosférica Patm, se trata de una presión diferencial o diferencia de presiones. A la presión relativa Prel se la conoce en inglés como gauge pressure Pg y viene dada por la relación:
Pabs = Patm + Pg
Prel = Pabs – Patm
Para la presión se utiliza el pascal como unidad de medida del Sistema Internacional de unidades, sin importar si se trata de una presión absoluta o de una presión relativa.
El pascal equivale a la fuerza ejercida por 1 newton sobre un área de 1 m2, pero otras unidades son de uso frecuente, como los milímetros de mercurio, de agua, las unidades anglosajonas como el psi y otras.
Si se conocen la presión absoluta en un punto y la presión atmosférica estándar, la presión relativa es la resta entre ambas.
Por ejemplo, supongamos que la presión absoluta en un cierto sistema es de 305 kPa. Sabiendo que la presión atmosférica estándar es de 101.3 kPa, la presión relativa es:
Pg = Pabs – Patm = 305 – 101.3 kPa = 203.7 kPa
El kPa o kilopascal es mil veces mayor que un pascal. Se usa con más frecuencia, ya que los valores de presión están en el orden de los miles de pascal. El peso de una manzana es aproximadamente 1 newton y un pascal equivale a esta fuerza repartida en un cuadrado de 1 metro de lado. También se usan otros múltiplos como el megapascal (1 MPa = 1 x 106 Pa) o el gigapascal (1 GPa = 1x 109 Pa).
La presión del ejemplo es manométrica, porque se encuentra por encima de la presión atmosférica, pero existen presiones absolutas por debajo de esta. Por ejemplo, si un gas en un recipiente tiene una presión absoluta de 50 kPa, su presión relativa es una presión de vacío que produce succión:
Pg = Pabs – Patm = 50 – 101.3 kPa = -51.3 kPa
En estos ejemplos se utilizó la presión atmosférica estándar, que es la presión existente a nivel del mar. Pero si se requiere una mayor exactitud en el cálculo, se puede utilizar la presión atmosférica local, la cual puede diferir de 101.3 kPa, ya que depende de la altitud y otras condiciones geográficas.
En los textos usualmente las presiones que se dan son relativas, y si se requiere trabajar con presiones absolutas, estas se distinguen con el uso de subíndices para evitar confusiones.
En cada punto del interior de un fluido como el agua hay presión. Suponiendo que el agua es incompresible, entonces su densidad se mantiene constante y la presión varía verticalmente.
Se puede comprobar tomando una pequeña porción de fluido en forma de disco de espesor dy que se encuentra en reposo en medio de la masa líquida.
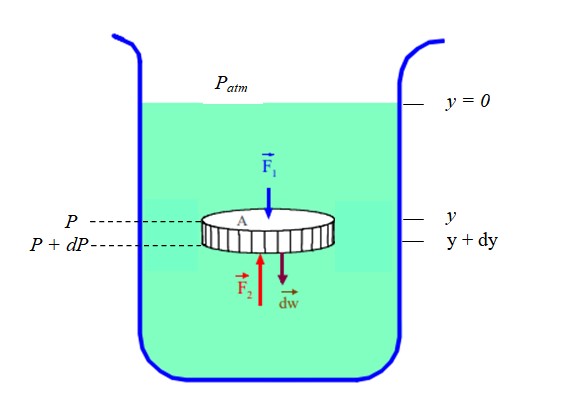
Las fuerzas sobre los bordes circulares del disco se cancelan por pares, no así las fuerzas que ejerce la masa de fluido por encima y por debajo del disco: F1 y F2. Además, es preciso considerar el peso del disco de fluido dW en la segunda ley de Newton:
∑Fy = F2 – F1 – W = 0
Dichas fuerzas se pueden expresar en términos de la presión, que es la fuerza perpendicular por unidad de área. De esta forma tenemos la presión P, producida por la fuerza F1:
F1 = P. A
Donde A es el área circular del disco. Análogamente:
F2 = (P + dP). A
Con P + dP la presión a la profundidad y + dy. El peso es dW = dm . g:
(P + dP). A – P. A – dm . g =0
La densidad del fluido es ρ = dm/ dV, con dV el volumen del disco de fluido, dado por A.dy. De esta manera:
(P + dP). A – P. A – ρA.dy .g =0
La ecuación obtenida se simplifica a:
dP – ρgdy = 0 → dP = ρgdy
Integrando a ambos lados desde y1 hasta y2:
= P2 – P1 = ρg (y2 – y1)
El término P2 – P1 es una diferencia de presiones o presión diferencial. Si queremos saber la presión en el punto de coordenada vertical y, hacemos y1 = 0, y2 = y y Po = Patm. Con esto tendremos la presión relativa a dicha profundidad, la cual depende únicamente de la profundidad y:
P2 – Patm = ρgy ⇒ Prel = ρgy
Todos hemos experimentado la presión que se siente al sumergirnos en una piscina o en el mar. ¿Cuál es la presión relativa que se siente al estar sumergido en una piscina de agua dulce a 5 metros de profundidad? Utilizando la expresión anterior, y sabiendo que la densidad del agua dulce es 1000 kg/m3, con g = 9.81 m/s2 la presión relativa es:
Prel = ρgy = 1000 x 9.81 x 5 Pa = 49050 Pa.
Los neumáticos de los vehículos suelen estar a una presión de 32 psi. Esta es una presión relativa o manométrica en libras por pulgada cuadrada, la unidad que se emplea en los países de habla inglesa. Muchos manómetros se calibran en estas unidades. 32 psi equivalen a 220632 Pa o 220 kPa.
Un tanque contiene gasolina y glicerina, dos líquidos no miscibles (no se mezclan) a las alturas indicadas. ¿Cuál es la presión manométrica en el fondo del tanque? Se anexan los pesos específicos, denotados con la letra griega γ, de cada fluido:
γgas = 45.3 lb/ft3
γgly = 78.7 lb/ft3
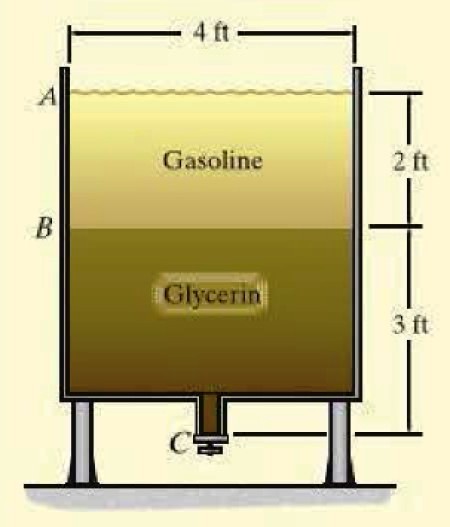
El peso específico γ de un fluido es el producto de su densidad por la aceleración de gravedad, por lo tanto la ecuación de la presión relativa se puede expresar así:
Prel = γ.y
La presión relativa en el fondo del tanque se debe tanto al peso de la columna de glicerina como el de la gasolina y es independiente de la forma del tanque:
Prel = γgas . yAB + γgly . yBC = (45.3 x 2 + 78.7 x 3) lb/ft2 = 326.7 lb/ft2
- Cimbala, C. 2006. Mecánica de Fluidos, Fundamentos y Aplicaciones. Mc. Graw Hill.
- Hibbeler, R. 2015. Fluid Mechanics. 1st. Ed. Pearson.
- Mott, R. 2006. Mecánica de Fluidos. 4ta. Edición. Pearson Educación.
- Smits, A. 2006. Mecánica de Fluidos, una introducción física. Alfaomega.
- Streeter, V. 1999. Mecánica de los Fluidos. McGraw Hill.
- Zapata, F. Presión y profundidad. Recuperado de: francesphysics.blogspot.com.
