Volumen atómico: qué es, cómo varía en la tabla periódica, ejemplos
¿Qué es el volumen atómico?
El volumen atómico es un valor relativo que indica la relación entre la masa molar de un elemento y su densidad. Entonces, este volumen depende de la densidad del elemento, y la densidad depende a su vez de la fase y de cómo se ordenan los átomos dentro de esta.
De manera que el volumen atómico para un elemento Z no es igual en otra fase distinta a la que exhibe a temperatura ambiente (líquida, sólida o gaseosa), o cuando forma parte de determinados compuestos. Así, el volumen atómico de Z en el compuesto ZA es diferente al del Z en el compuesto ZB.
¿Por qué? Para comprenderlo es necesario comparar los átomos con, por ejemplo, unas canicas. Las canicas tienen muy bien definidas su frontera material, la cual se observa gracias a su brillante superficie. En cambio, la frontera de los átomos es difusa, aunque puedan considerarse remotamente esféricos.
Así, lo que determina un punto más allá de la frontera atómica es la probabilidad nula de encontrar un electrón, y este punto puede estar más lejos o más cerca del núcleo dependiendo de cuántos átomos vecinos interactúan alrededor del átomo en consideración.
Volumen y radio atómicos
Al interaccionar dos átomos H en la molécula H2, las posiciones de sus núcleos están definidas así como las distancias entre estos (distancias internucleares). Si ambos átomos son esféricos, el radio es la distancia entre el núcleo y la frontera difusa:
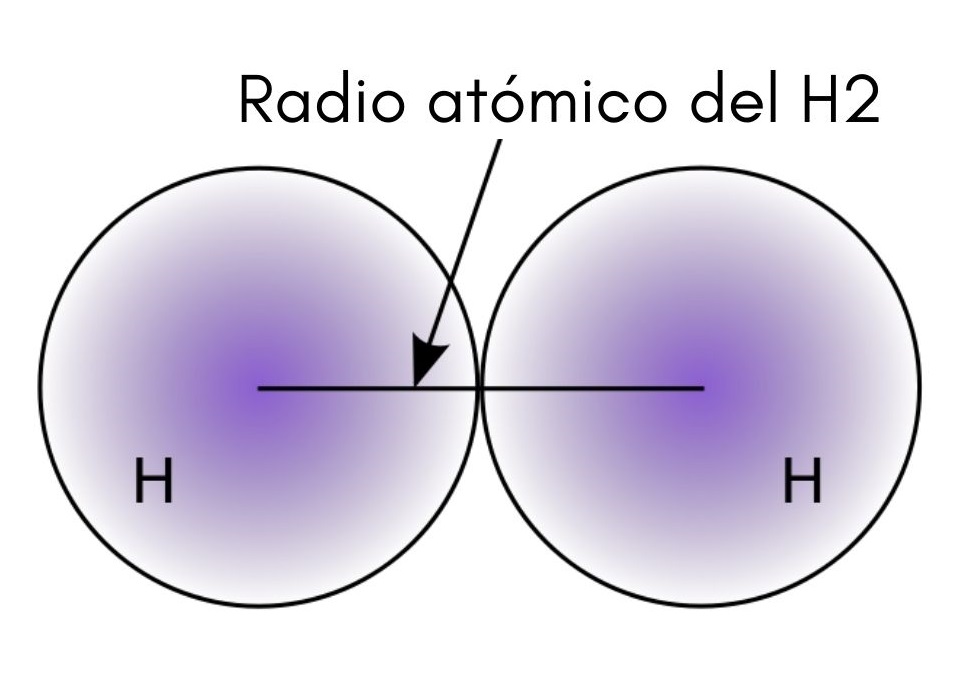
En la imagen superior puede apreciarse cómo la probabilidad de hallar un electrón decrece conforme se aleja del núcleo. Dividiendo entonces entre dos la distancia internuclear, se obtiene el radio atómico. Seguidamente, asumiendo una geometría esférica para los átomos, se recurre a la fórmula para calcular el volumen de una esfera:
V= (4/3)(Pi)r3
En esta expresión r es el radio atómico determinado para la molécula de H2. El valor de V calculado por este método poco preciso puede cambiar si, por ejemplo, se considerase H2 en estado líquido o metálico. No obstante, este método es muy inexacto debido a que las formas de los átomos se alejan mucho de la esfera ideal en sus interacciones.
Para determinar los volúmenes atómicos en los sólidos se toman en cuenta muchas variables concernientes al arreglo, y que se obtienen por estudios de difracción de rayos X.
Fórmula adicional
La masa molar expresa la cantidad de materia que posee un mol de átomos de un elemento químico.
Sus unidades son g/mol. Por otra parte, la densidad es el volumen que ocupa un gramo del elemento: g/mL. Debido a que las unidades del volumen atómico son mL/mol, hay que jugar con las variables para llegar a las unidades deseadas:
- (g/mol)(mL/g)= mL/mol
O lo que es igual:
- (Masa molar)(1/D) =V
- (Masa molar/D)= V
Así, fácilmente puede calcularse el volumen de un mol de átomos de un elemento; mientras que con la fórmula del volumen esférico se calcula el volumen de un átomo individual.
Para llegar a este valor a partir del primero es necesaria una conversión a través del número de Avogadro (6,02·10-23).
¿Cómo varía el volumen atómico en la tabla periódica?
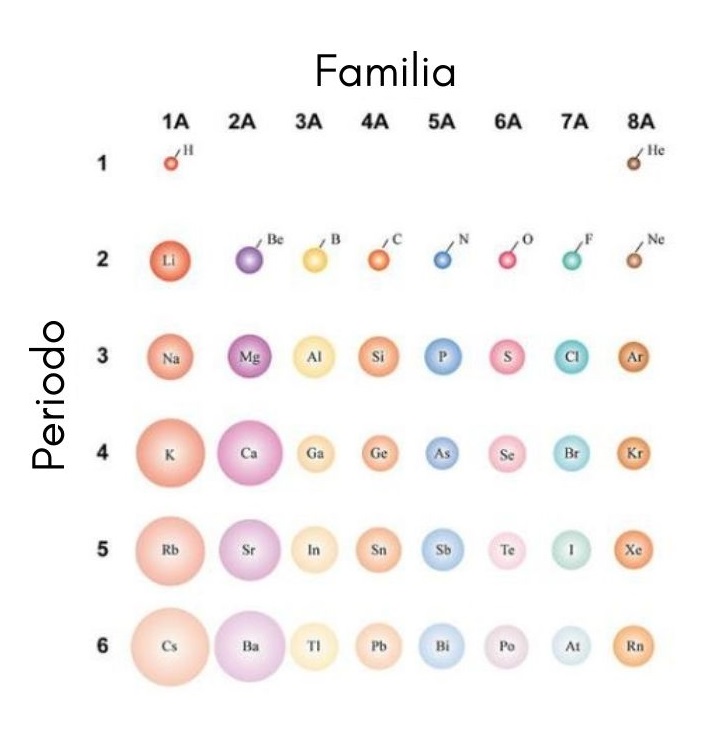
Si los átomos se consideran esféricos, entonces su variación será la misma que se observa en los radios atómicos. En la imagen superior, que muestra de los elementos representativos, se ilustra que de derecha a izquierda los átomos empequeñecen; en cambio, de arriba hacia abajo estos se tornan más voluminosos.
Esto se debe a que en un mismo período el núcleo incorpora protones conforme se desplaza a la derecha. Estos protones ejercen sobre los electrones externos una fuerza de atracción, los cuales sienten una carga nuclear efectiva Zef, menor a la carga nuclear real Z.
Los electrones de las capas internas repelen a los de la capa externa, disminuyendo el efecto del núcleo sobre estos; esto se conoce como el efecto pantalla. En un mismo período el efecto pantalla no logra contrarrestar el aumento del número de protones, por lo que los electrones de la capa interna no impiden la contracción de los átomos.
Sin embargo, al descender en un grupo se habilitan nuevos niveles energéticos, los cuales permiten que los electrones orbiten más alejados del núcleo. Asimismo, se incrementan el número de electrones de la capa interna, cuyos efectos de apantallamiento empieza a verse disminuido si el núcleo vuelve a sumar protones.
Por estas razones se aprecia que el grupo 1A tiene los átomos más voluminosos, a diferencia de los átomos pequeños del grupo 8A (o 18), el de los gases nobles.
Volúmenes atómicos de los metales de transición
Los átomos de los metales de transición incorporan electrones a los orbitales internos d. Este incremento del efecto pantalla y, así como de la carga nuclear real Z, se anulan casi igualitariamente, por lo que sus átomos conservan el tamaño similares en un mismo período.
En otras palabras: en un período, los metales de transición exhiben volúmenes atómicos similares. No obstante, estas pequeñas diferencias son enormemente significativas al momento de definir los cristales metálicos (como si fueran canicas metálicas).
Ejemplos de volumen atómico
Están disponibles dos fórmulas matemáticas para calcular el volumen atómico de un elemento, cada una con sus ejemplos correspondientes.
Ejemplo 1
Dado el radio atómico del hidrógeno —37 pm (1 picómetro= 10-12m)— y del cesio —265 pm—, calcule sus volúmenes atómicos.
Recurriendo a la fórmula del volumen esférico, se tiene entonces:
VH= (4/3)(3.14)(37 pm)3= 212,07 pm3
VCs= (4/3)(3.14)(265 pm)3=77912297,67 pm3
Sin embargo, esos volúmenes expresados en picómetros resultan exorbitantes, por lo que se transforman en unidades de angstroms, multiplicándolos por el factor de conversión (1Å/100pm)3:
(212,07 pm3)(1Å/100pm)3= 2,1207×10-4 Å3
(77912297,67 pm3)(1Å/100pm)3= 77,912 Å3
Así, quedan numéricamente evidenciadas las diferencias de tamaño entre el pequeño átomo de H y el voluminoso átomo de Cs. Es preciso tener en cuenta que estos cálculos no son más que aproximaciones bajo la afirmación de que un átomo es totalmente esférico, la cual divaga frente a la realidad.
Ejemplo 2
La densidad del oro puro es de 19,32 g/mL y su masa molar es 196,97 g/mol. Aplicando la fórmula M/D para calcular el volumen de un mol de átomos de oro se tiene lo siguiente:
VAu= (196,97 g/mol)/(19,32 g/mL)= 10,19 mL/mol
Es decir, que 1 mol de átomos de oro ocupa 10,19 mL, pero ¿qué volumen ocupa un átomo de oro específicamente? ¿Y cómo expresarlo en unidades de pm3? Para esto sencillamente basta con aplicar los siguientes factores de conversión:
(10,19 mL/mol)·(mol/6,02·10-23 átomos)·(1 m/100 cm)3·(1 pm/10-12m)3= 16,92 ·106 pm3
Por otro lado, el radio atómico del oro es 166 pm. Si se comparan ambos volúmenes —el obtenido por el método anterior y el que se calcula con la fórmula del volumen esférico— se encontrará que no tienen el mismo valor:
VAu= (4/3)(3.14)(166 pm)3= 19,15·106 pm3
¿Cuál de los dos se acerca más al valor aceptado? Aquel que es más próximo a los resultados experimentales obtenidos por difracción de rayos X de la estructura cristalina del oro.
