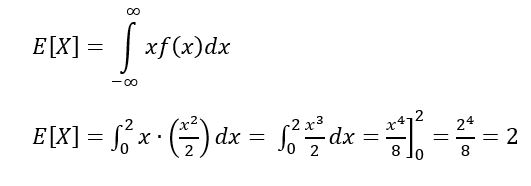Variable aleatoria continua: qué es, características, ejemplos, ejercicios

¿Qué es una variable aleatoria continua?

Una variable aleatoria continua es un valor numérico obtenido al azar, el cual resulta de hacer un experimento y que puede tomar infinitos valores. Esto significa que, conocidos dos valores consecutivos de la variable, siempre es posible encontrar otro valor intermedio entre ellos.

Al tener una cantidad infinita de valores, la colección de valores de la variable continua no es contable y casi siempre pertenecen al conjunto de los números reales.

Ejemplos de este tipo de variables son la estatura, el peso y la temperatura corporal de una persona, pero se puede definir un sinnúmero de ellas, más abajo se encontrarán varios ejemplos. En contraste con la variable aleatoria continua, está la variable aleatoria discreta, que sí es contable, como el número de hijas en una familia, o cuántos automóviles vende una agencia al cabo de un mes.

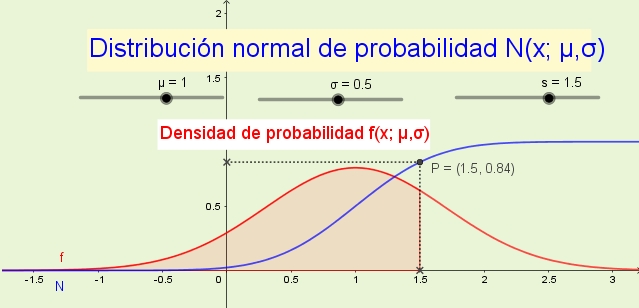
Una variable aleatoria continua se denota mediante una letra mayúscula como la X, y los infinitos valores que toma la variable son los posibles resultados del experimento aleatorio:

X = {x₁, x₂, x₃, … ∞}

Cada valor tiene una cierta probabilidad de ocurrencia, y al modelo mediante el cual se calcula dicha probabilidad, se le denomina distribución de probabilidad.

Pero, dado que X toma infinitos valores, no se puede calcular la probabilidad para valores puntuales de la variable. Entonces, es necesario definir una función F(x), llamada función de distribución acumulada, o simplemente función de distribución, según la cual se calcula la probabilidad acumulada hasta un determinado valor o entre dos valores:

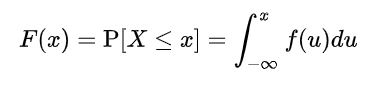
Donde f(u) recibe el nombre de función de densidad. Definida de esta forma, F(x) representa la probabilidad de que X se encuentre entre –∞ y x.

Características de una variable aleatoria continua

Las variables aleatorias continuas quedan completamente definidas al conocer el conjunto de valores que puede tomar y la probabilidad de ocurrencia de cada uno, dada a través de su función de densidad f(x).

La función de densidad f(x) debe cumplir las siguientes propiedades:

• La función f(x) es positiva: f(x) >= 0
• El área bajo la curva y = f(x) siempre es igual a 1, es decir que la probabilidad de ocurrencia de algún resultado x en el intervalo (-∞, +∞) es del 100%.
• La probabilidad de que X se encuentre en el intervalo [a, b] se calcula mediante la siguiente integral definida:

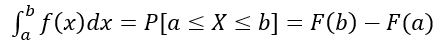
La cual equivale al área bajo la curva y = f(x), comprendida entre a y b. Además:

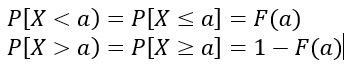
Los valores de f(x) no representan una probabilidad, por lo que P [x = c] = 0. Los valores relevantes son los que corresponden al área bajo la curva y = f(x), los cuales representan una probabilidad.

• Al derivar la función de distribución F(x) con respecto a x, se obtiene f(x).

La gráfica de f(x) para una variable aleatoria continua, es análoga a la poligonal de frecuencias que se construye para una variable estadística discreta, con la diferencia de que, para la variable aleatoria, el ancho del intervalo se hace infinitesimal.

Esperanza

La esperanza es una de las medidas características de una variable continua. La esperanza o valor esperado de X indica el valor que se espera que ocurra con más frecuencia, y se calcula a través de la siguiente integral:

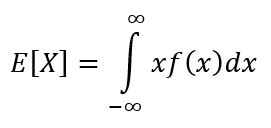
Sus propiedades son:

• E[a∙x] = a∙E[x]
• E[X+Y] = E[X] + E[Y]
• E[a∙X+b∙Y] = a∙E[X] + b∙E[Y]

Donde las cantidades a y b son números reales.

Ejemplos

Como se indicó previamente, hay muchísimas situaciones en las que se puede definir una o más variables aleatorias continuas. En ciencia y otras áreas, las más comunes son de tiempo, longitud, peso, volumen y temperatura:

Tiempos

Con la finalidad de optimizar procesos y servicios, se diseñan experimentos que estudian el tiempo que tardan estos en llevarse a cabo:

X = Tiempo que tarda un cliente ante la ventanilla del banco.

Y = Lo que demora un local de comida rápida en servir una orden.

Z = Tiempo en que se produce una determinada reacción química.

Estaturas y pesos

En muchos estudios sobre personas y animales, la estaturas y pesos son relevantes:

X = Altura de las niñas en un curso de 6to. Grado en cada colegio de una ciudad.

Y = Peso de los bebés al nacer en un hospital público.

Z = El peso de las vacas en una granja.

Temperaturas

La temperatura es un parámetro relevante en numerosos procesos químicos, que suele tomar infinitos valores en un determinado rango:

X = Temperatura a la que ocurre una determinada reacción química, sabiendo que esta ocurre entre 80 ºC y 120 ºC.

Ejercicios resueltos

Ejercicio 1

Determinar cuáles son las variables aleatorias continuas:

1. La cantidad de estudiantes que atiende el cafetín de la universidad al día.
2. Presión arterial de los pacientes que acuden a una sala de emergencias.
3. Longitud de las alas de aves, de una especie en peligro de extinción, que habitan en una reserva.
4. Tiempo transcurrido entre que una persona y otra es atendida en un banco.
5. Cantidad de productos defectuosos al mes en una fábrica.
6. Niveles de colesterol en los pollos de una granja.
7. Cantidad de farolas que funcionan en una calle, de un total de 12.

Solución

1.- La cantidad de estudiantes atendidos al día es numerable, por lo tanto, esta variable no es continua, sino discreta.

2.- Es continua. La presión arterial de los pacientes puede tomar cualquier valor en un rango dado.

3.- Variable continua, puesto que la longitud del ala de un ave toma cualquier valor entre un mínimo y un máximo, según la especie.

4.- El tiempo que transcurre entre atenciones a clientes es variable y puede tomar cualquier valor en un rango determinado, por ejemplo, entre 1 y 5 minutos.

5.- Como el número de productos defectuosos es contable, se trata de una variable aleatoria discreta.

6.- Esta variable es continua, ya que el nivel de colesterol en los pollos toma cualquier valor en un rango previamente determinado.

7.- Discreta. El número de farolas del alumbrado que funcionan es una cantidad contable.

Ejercicio 2

Se define la variable aleatoria continua X = “nivel de colesterol” en cierta variedad de pollos de una granja, la cual tiene la siguiente función de densidad f(x):

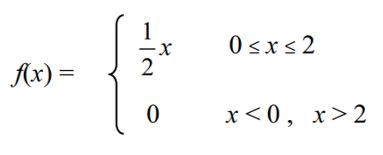
Calcular lo siguiente:

1. F(x)
2. P [X ≤2]
3. La esperanza E[X]

Solución a

De acuerdo a la definición dada al comienzo:

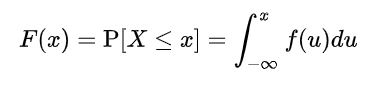
Por lo tanto, F(x) es una función por partes. Para el intervalo x0, F(x) es igual a 0, por las propiedades enunciados al comienzo.

En el intervalo 0≤x≤2, se resuelve la integral indefinida:

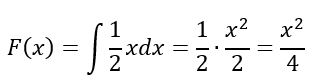
Por último, para el intervalo x>2, F(x) = 1, según las propiedades, por lo tanto, F(x) queda así:

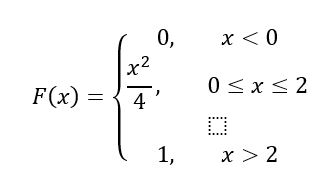
Solución b

La probabilidad buscada es F (1.2) y como x= 1.2 se encuentra entre 0≤x≤2, se toma esa parte de F(x) para evaluar:

F(1.2) = ¼ ∙ (1.2)² = 0.36.

Solución c

Para calcular la esperanza o valor esperado, se utiliza: