Cuadrado
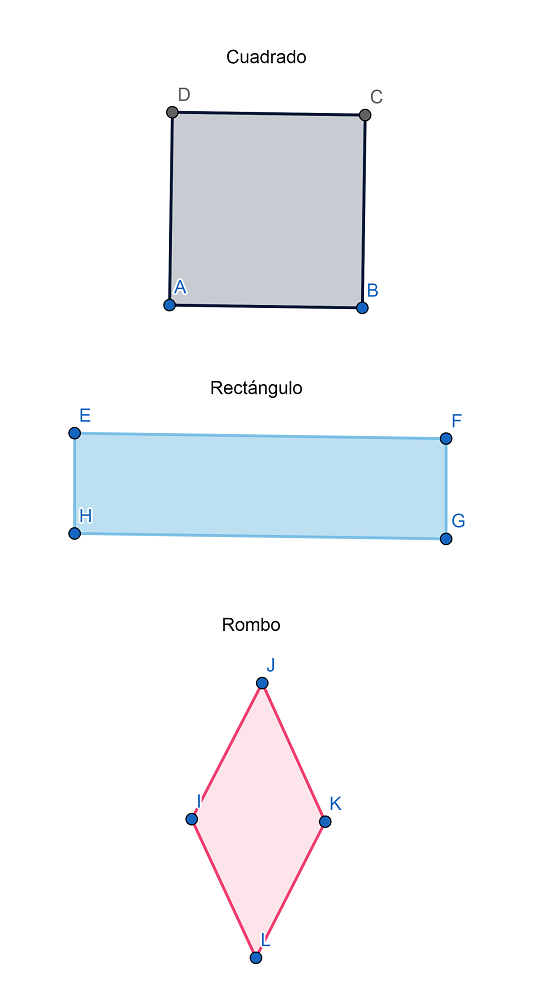
El cuadrado es una figura geométrica caracterizada por ser un tipo de paralelogramo con cuatro lados de igual longitud y paralelos entre sí.
Un cuadrado es entonces un polígono regular. Esto quiere decir que todos sus lados son idénticos, y además todos sus ángulos interiores miden lo mismo (en este caso, 90º).
Como ya mencionamos, el cuadrado es una categoría de paralelogramo que, a su vez, es un tipo de cuadrilátero donde los lados opuestos son paralelos entre sí (no se cruzan aunque sean prolongados). Sin embargo, un paralelogramo no necesariamente tiene todos sus lados iguales, como es el caso del rectángulo, donde solo los lados opuestos tienen la misma longitud.
Otro caso de paralelogramo es el rombo, donde todos los lados tienen la misma longitud, pero solo un par de ángulos son congruentes (miden lo mismo).
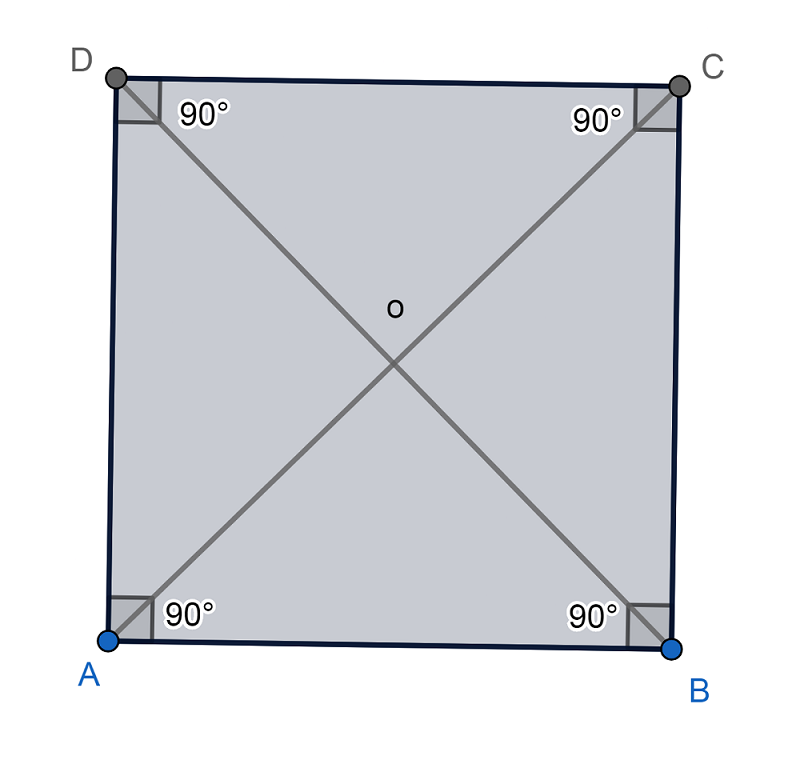
Elementos del cuadrado
Los elementos del cuadrado, como observamos en el gráfico inferior, son los siguientes:
- Vértices: A, B, C, D.
- Lados: AB, BC, DC, AD.
- Diagonales: AC,DB.
- Ángulos interiores: Son iguales y miden 90º.
- Centro o centroide (o): Es el punto donde se cruzan las diagonales.
Perímetro, diagonal y área del cuadrado
Las fórmulas para conocer las características del cuadrado son las siguientes:
- Perímetro(P): Si a es la longitud de lado del cuadrado (como se observa en el gráfico de arriba), el perímetro sería: P = 4*a
- Diagonal: Debemos recordar que las diagonales dividen al cuadrado en dos triángulos iguales que son triángulos rectángulos isósceles. Es decir, están formados por un ángulo recto de 90º y dos ángulos menores que 90º. El ángulo recto está constituido por la unión de dos lados llamados catetos. En tanto, el lado del triángulo que es opuesto al ángulo recto se denomina hipotenusa. Entonces, si tomamos, como referencia la figura de abajo, el triángulo formado por los vértices A, B y D (el área sombreada), la hipotenusa sería el lado DB, mientras que los catetos son AB y AD.
El teorema de Pitágoras nos indica que si elevamos al cuadrado los catetos y los sumamos, obtendremos la hipotenusa al cuadrado, como vemos en la siguiente fórmula (donde d es la longitud de la diagonal y a es la longitud del lado del cuadrado):
- Área (A): El área se calcula multiplicando la base por la altura, que en el caso del cuadrado miden lo mismo y son iguales a la longitud del lado (a):
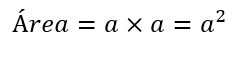
Para hallar el área en función a la longitud de la diagonal, reemplazamos a por d, tomando en cuenta que:
Por lo tanto, el área sería:
Ejemplo de cuadrado
Supongamos que tenemos un cuadrado con un lado que mide 16 metros. Podemos entonces hallar el perímetro (P), la diagonal (d) y el área (A).
Propiedades relativas a la circunferencia inscrita o circunscrita
Cabe señalar que la diagonal del cuadrado es igual al diámetro de la circunferencia circunscrita a él (que en el gráfico inferior está dibujada de color celeste).
Asimismo, el lado del cuadrado es igual al diámetro de la circunferencia inscrita a este (que en el gráfico de abajo está dibujada de color fucsia).
Vale recordar que el diámetro es la recta que atraviesa el centro de una circunferencia y une dos puntos opuestos de dicha figura.
