Vector unitario

En otras palabras, un vector unitario es un vector que tiene dirección y sentido con una magnitud igual a uno pero es adimensional.

El módulo de un vector es la magnitud de un segmento orientado en un espacio que está determinado por dos puntos y el orden de estos. Simplificando, el módulo de un vector es la longitud entre el inicio y el final del vector, es decir, dónde empieza y dónde termina la flecha.

Dado un vector v de dos dimensiones con coordenadas (v1,v2), el módulo sería tal que:

La característica principal de un vector unitario es que el módulo es igual a uno y que es adimensional. La propiedad de adimensionalidad se debe a que este vector no tiene prestablecida ninguna dimensión por sí mismo.

Esta característica está presente en la normalización de un vector donde se pretende encontrar un vector con el mismo sentido y dirección con módulo igual a uno (vector unitario) a partir de un vector distinto de cero dado.

Por tanto, como este vector unitario dependerá de las dimensiones del vector de referencia, el vector unitario se adaptará y tomará dichas dimensiones. En consecuencia, hablaremos de adimensionalidad porque previamente no hay ninguna dimensión establecida hasta que queda determinada por el vector de referencia. 

El vector unitario también recibe el nombre de vector normalizado por la acción de normalizar un vector. Este proceso consiste en encontrar un vector con la misma dirección y sentido que el vector que queremos normalizar, pero especialmente con módulo igual a 1.

En otras palabras, partimos de un vector distinto de cero y replicamos su dirección y sentido, pero manteniendo que su módulo sea igual a uno. El resultado final son dos vectores: el vector original y el vector unitario con la misma dirección y sentido que el vector original, pero con módulo igual a uno.

Es habitual encontrar al vector unitario expresado mediante una letra y con un acento circunflejo, de la forma: â. También se puede representar mediante la letra griega mu y un subíndice que indica el vector el cual se replica su dirección y sentido.

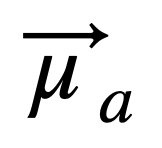
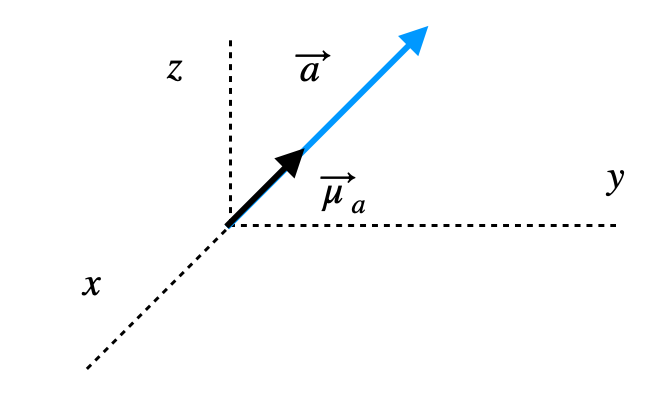
En el plano cartesiano de tres dimensiones anterior se puede ver el vector unitario y un vector cualquiera distinto de cero. Podemos apreciar que el vector unitario tiene la misma dirección y sentido que el vector a, pero un módulo distinto.  

Determina si los siguientes módulos de vectores pertenecen a vectores unitarios:

El único módulo que pertenece a un vector unitario es el último módulo que corresponde al vector d.