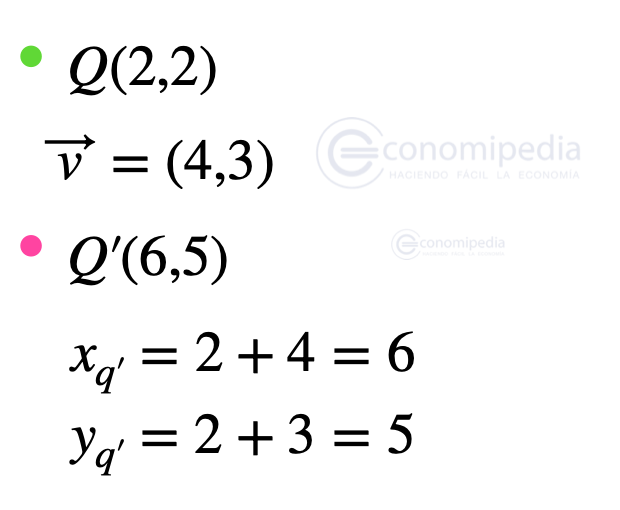Traslación de vectores
La traslación de vectores en el plano es una aplicación a un punto mediante un vector llamado vector de traslación, resultando en un punto denominado punto homólogo.
En otras palabras, la traslación de vectores es desplazar un punto a través de sumar las coordenadas del vector de traslación y obtener otro punto llamado punto homólogo.
Se denomina modificación o transformación puntual ya que la traslación se aplica a un punto en el plano a través de un vector.
Procedimiento de la traslación de vectores
Para hacer una traslación de vectores necesitamos:
- Un punto en el plano.
- Un vector que nos dictará la traslación del punto.
- Hacer la traslación: obtención del punto homólogo.
Una vez aplicados los dos primeros pasos anteriores obtendremos un punto denominado punto homólogo (paso 3). Este punto es el resultado de hacer la traslación del punto inicial. Entonces, para poder hacer la traslación de un vector es imprescindible tener un punto y un vector, en caso contrario, no podremos hacer la traslación.
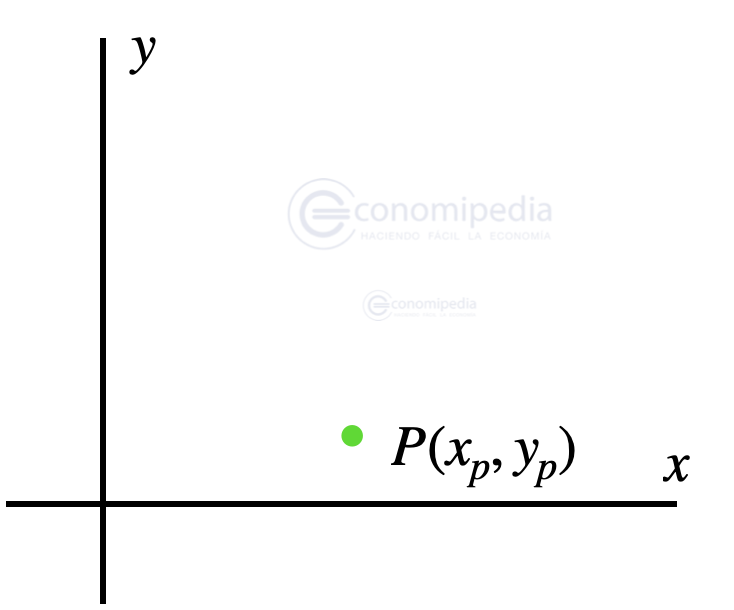
Primer paso: Tener un punto
Suponemos que tenemos un punto inicial llamado P y que tiene unas coordenadas de x e y. Le añadimos el subíndice p para remarcar que esas coordenadas pertenecen al punto P.
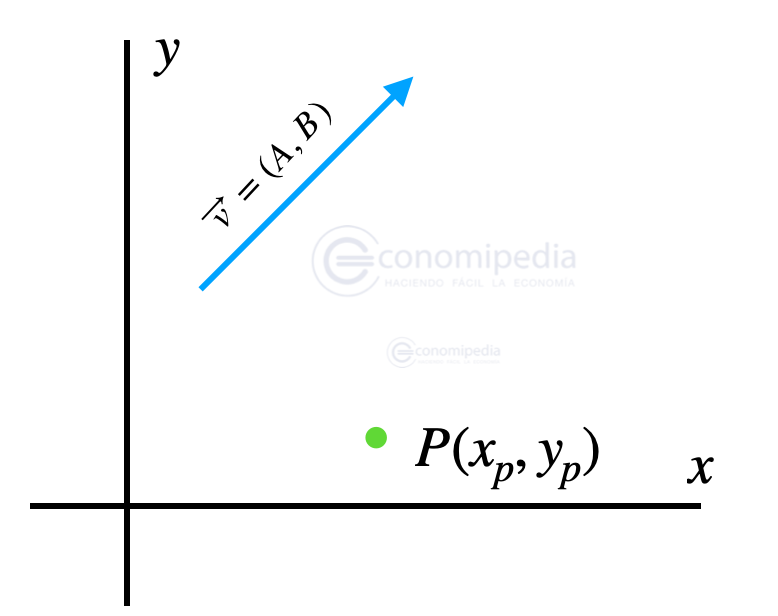
Segundo paso: Tener un vector
También, suponemos que tenemos un vector llamado v que está comprendido entre los puntos A y B.
Tercer paso: Hacer la traslación
Una vez tenemos controlados el punto y el vector a partir del cual aplicaremos la traslación, solo nos falta calcular el punto homólogo. El punto homólogo se calcula haciendo la suma de las coordenadas del vector y el punto inicial. En nuestro caso, tendríamos que escribir las coordenadas del punto inicial P y sumarle las coordenadas del vector v.
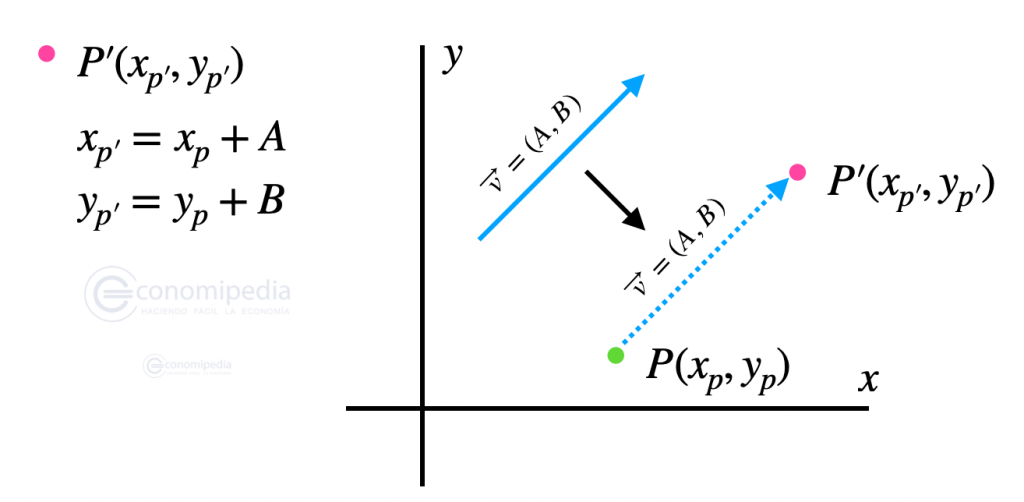
El punto rosa corresponde al punto homólogo al punto P. Para obtener las coordenadas del punto homólogo tenemos que sumar las coordenadas del vector v a las coordenadas del vector inicial P.
Podemos ver en el gráfico como se encuentra el punto homólogo con la traslación del punto P mediante el vector v. A través de la suma de las coordenadas estamos trasladando el punto P en otra situación en el plano que cumple con las coordenadas del vector v.
Traslación de vectores aplicada a figuras
De la misma forma que se ha aplicado la traslación a un punto en concreto, también puede aplicarse a un conjunto de puntos. Si este conjunto de puntos está unido por segmentos y está cerrado hablaremos de una figura. Entonces, puede aplicarse la traslación de figuras geométricas en el plano.
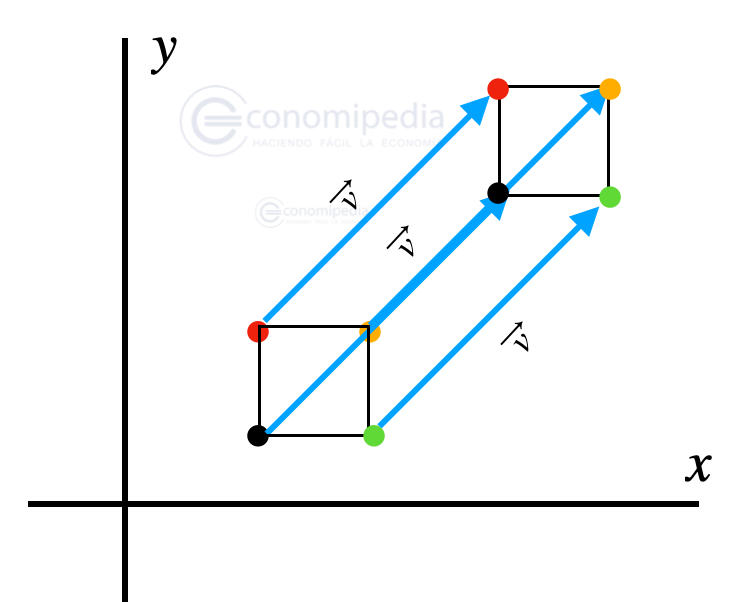
Ejemplo de traslación de vectores
Aplica la traslación al siguiente punto mediante el siguiente vector: