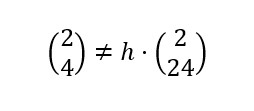Transformación lineal de matrices
La transformación lineal de matrices son operaciones lineales mediante matrices que modifican la dimensión inicial de un vector dado.
En otras palabras, podemos modificar la dimensión de un vector multiplicándolo por una matriz cualquiera.
Las transformaciones lineales son la base de los vectores y valores propios de una matriz dado que dependen linealmente unos de otros.
Artículos recomendados: operaciones con matrices, vectores y valores propios.
Matemáticamente
Definimos una matriz C cualquiera de dimensión 3×2 multiplicada por un vector V de dimensión n=2 tal que V=(v1,v2).
¿De qué dimensión será el vector resultado?
El vector resultado del producto de la matriz C3×2con el vector V2×1será un nuevo vector V’ de dimensión 3.
Este cambio de dimensión del vector es debido a la transformación lineal mediante la matriz C.
Ejemplo práctico
Dada la matriz cuadrada R con dimensión 2×2 y el vector V de dimensión 2.
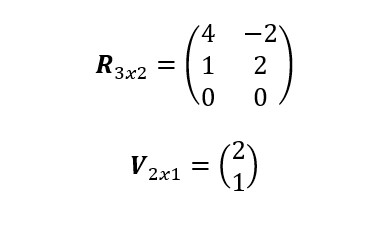
Una transformación lineal de la dimensión del vector V es:
donde la dimensión inicial del vector V era 2×1 y ahora la dimensión final del vector V es3×1. Este cambio de dimensión se consigue mediante la multiplicación de la matriz R.
¿Estas transformaciones lineales pueden representarse gráficamente? ¡Pues claro!
Representaremos el vector resultado V’ en un plano.
Entonces:
V = (2,1)
V’ = (6,4)
Gráficamente
Vectores propios mediante representación gráfica
¿Cómo podemos determinar que un vector es un vector propio de una matriz dada con tan solo mirando la gráfica?
Definimos la matriz D de dimensión 2×2:
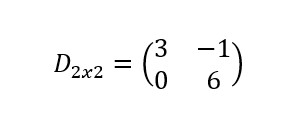
¿Son los vectores v1=(1,0) y v2=(2,4) vectores propios de la matriz D?
Procedimiento
1. Empecemos por el primer vector v1. Hacemos la transformación lineal anterior:
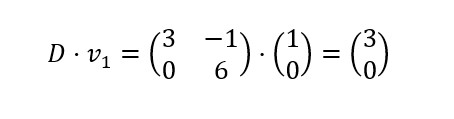
Entonces, si realmente el vector v1 es vector propio de la matriz D, el vector resultante v1’ y vector v1deberían pertenecer a la misma recta.
Representamos v1 = (1,0) y v1’ = (3,0).
Dado que tanto v1como v1’ pertenecen a la misma línea, v1 es un vector propio de la matriz D.
Matemáticamente, existe una constante h(valor propio) tal que:
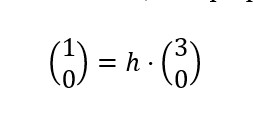
2. Seguimos con el segundo vector v2. Repetimos la transformación lineal anterior:
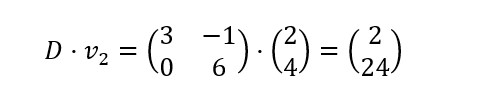
Entonces, si realmente el vector v2 es vector propio de la matriz D, el vector resultante v2’ y el vector v2 deberían pertenecer a la misma recta (como la gráfica anterior).
Representamos v2 = (2,4) y v2’ = (2,24).
Dado que v2 y v2’ no pertenecen a la misma línea, v2 no es un vector propio de la matriz D.
Matemáticamente, no existe una constante h(valor propio) tal que: