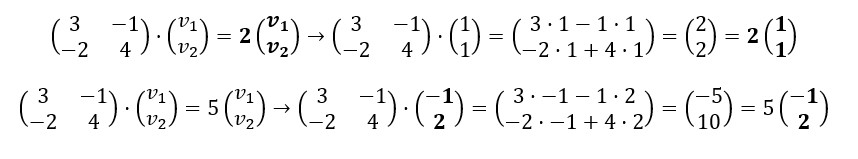Vectores y valores propios
Los vectores propios son vectores multiplicados por un valor propio en las transformaciones lineales de una matriz. Los valores propios son constantes que multiplican los vectores propios en las transformaciones lineales de una matriz.
En otras palabras, los vectores propios traducen la información de la matriz original en la multiplicación de valores y una constante. Los valores propios son esta constante que multiplica los vectores propios y que participa en la transformación lineal de la matriz original.
A pesar de que su nombre en español es muy descriptivo, en inglés, los vectores propios se denominan eigenvectors y los valores propios, eigenvalues.
Artículos recomendados: tipologías de matrices, matriz inversa, determinante de una matriz.
Vectores propios
Los vectores propios son conjuntos de elementos que mediante la multiplicación de una constante cualquiera, son equivalentes con la multiplicación de la matriz original y los conjuntos de elementos.
Matemáticamente, un vector propio V=(v1,…,vn) de una matriz cuadrada Q es cualquier vector V que satisface la siguiente expresión para cualquier constante h:
QV = hV
Valores propios
La constante h es el valor propio que pertenece al vector propio V.
Los valores propios son las raíces reales (raíces que tienen como solución números reales) que encontramos mediante la ecuación característica.
Características de los valores propios
- Cada valor propio tiene infinitos vectores propios dado que existen infinitos números reales que pueden formar parte de cada vector propio.
- Son escalares, pueden ser números complejos (no reales) y pueden ser idénticos (más de un valor propio iguales).
- Existen tantos valores propios como número de filas (m) o columnas (n) tiene la matriz original.
Vectores y valores propios
Entre vectores y valores propios existe una relación de dependencia lineal dado que los valores propios multiplican los vectores propios.
Matemáticamente
Si V es un vector propio de la matriz Z y h es el valor propio de la matriz Z, entonces hV es una combinación lineal entre vectores y valores propios.
Función característica
La función característica se utiliza para encontrar los valores propios de una matriz Z cuadrada.
Matemáticamente
(Z – hl) · V = 0
Donde Zy h están definidas anteriormente y I es la matriz identidad.
Condiciones
Para encontrar vectores y valores propios de una matriz, se debe cumplir:
- Matriz Z cuadrada: el número de filas (m) es el mismo que el número de columnas (n).
- Matriz Z real. La mayoría de las matrices utilizadas en finanzas tienen raíces reales. ¿Qué ventaja existe en la utilización de raíces reales? Pues que los valores propios de la matriz nunca van a ser números complejos, y eso amigos, nos soluciona mucho la vida.
- Matriz (Z– hI) no invertible: determinante = 0. Esta condición nos ayuda a encontrar siempre vectores propios distintos de cero. Si encontrásemos vectores propios iguales a 0, entonces la multiplicación entre valores y vectores propios sería nula.
Ejemplo práctico
Suponemos que queremos encontrar los vectores y valores propios de una Z matriz de dimensión 2×2:
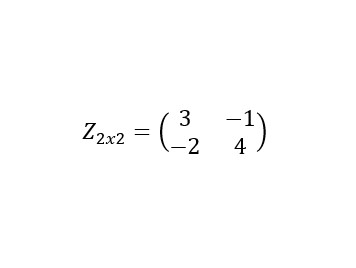
1. Sustituimos la matriz Z y I en la ecuación característica:
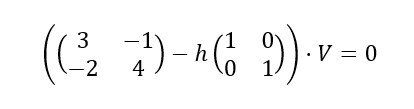
2. Arreglamos los factores:
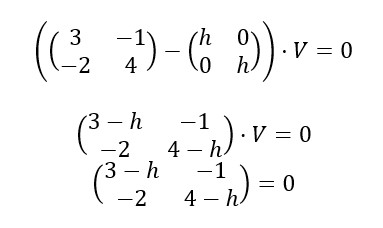
3. Multiplicamos los elementos como si buscásemos el determinante de la matriz.
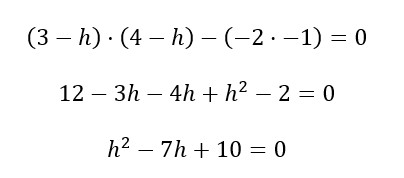
4. La solución de esta ecuación cuadrática es h=2 y h=5. Dos valores propios porque el número de filas o columnas de la matriz Z es 2. Entonces, hemos encontrado los valores propios de la matriz Z que a la vez hacen que el determinante sea 0.
5. Para encontrar los vectores propios tendremos que resolver:
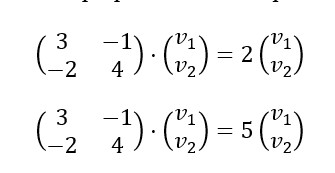
6. Por ejemplo, (v1,v2)=(1,1) para h=2 y (v1,v2)=(-1,2) para h=5: