Tetraedro
El tetraedro es un poliedro con cuatro caras, seis aristas y cuatro vértices. Se trata de una figura tridimensional formada por varios polígonos que, en este caso, son triángulos.
El tetraedro se caracteriza por ser el más simple de los poliedros, y el único que posee menos de cinco lados.
Vale precisar que un tetraedro es una pirámide con base triangular.
Elementos de un tetraedro
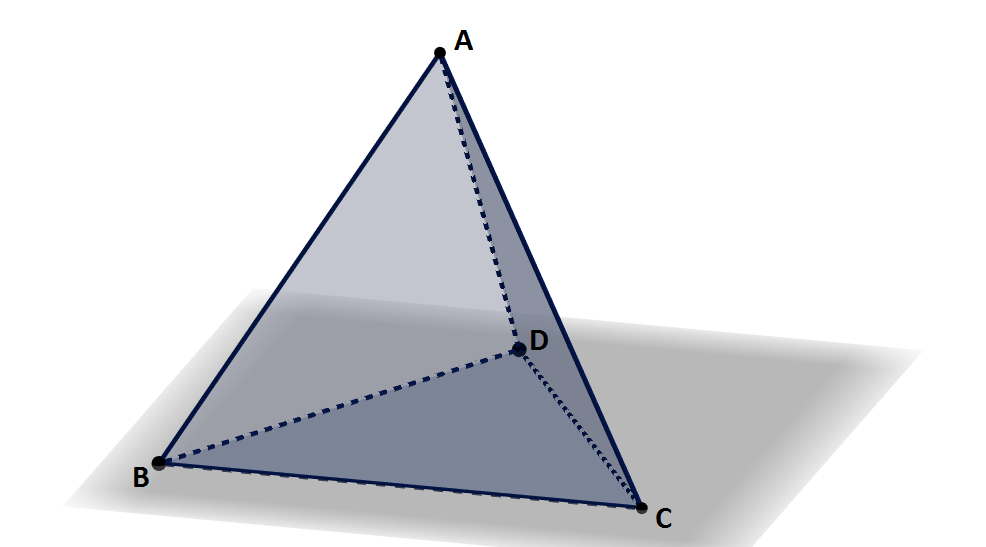
Los elementos de un tetraedro, guiándonos de la figura de abajo, son:
- Caras: Son los lados del tetraedro que, como mencionamos, son triángulos (ABC, ADC, ADB y BDC.
- Aristas: Es la unión de dos caras: AB, AC, AD, BC, CD y DB.
- Vértices: Son aquellos puntos donde se unen las aristas: A, B, C y D.
- Ángulo diedro: Se forma por la unión de dos caras.
- Ángulo poliedro: Es aquel que se constituye por los lados que coinciden en un solo vértice.
Área y volumen del tetraedro
Para conocer las características del tetraedro podemos calcular:
- Área: Se tendría que sumar el área de los cuatro triángulos que conforman el poliedro. En ese sentido, debemos recordar que él área de un triángulo se calcula multiplicando la base por la altura y dividiendo entre 2 ( A=bxh/2)
- Volumen: Se calcularía con la siguiente fórmula
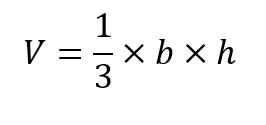
En la fórmula, b es una cara cualquiera del poliedro y h es la altura o segmento que une b con su vértice opuesto. Además, la altura es perpendicular a la base (forman un ángulo recto o que mide 90º).
Tetraedro regular
Cuando todos los triángulos que forman el tetraedro son triángulos equiláteros idénticos entre sí, nos encontramos ante un tetraedro regular. Es decir, sería un caso de un poliedro regular, cuyas caras son todas iguales y además cada una es un polígono regular.
En este punto, debemos recordar que un polígono regular es aquel donde todos los lados tienen la misma longitud y además sus ángulos interiores también son todos iguales.
Recordemos entonces que el área (A) de un triángulo equilátero se puede calcular utilizando fórmula de Herón donde a, b y c son las medidas de los lados y s es el semiperímetro, que es el perímetro (P) entre dos.
Entonces, si:
P = a + b + c = a + a + a = 3a
Tenemos que:
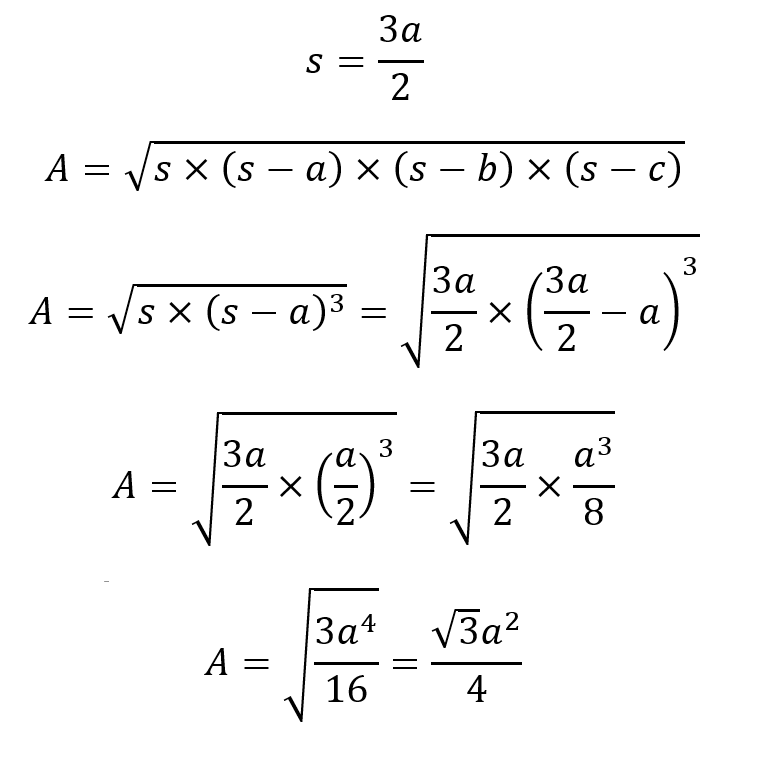
Luego, como son cuatro triángulos, multiplicamos el área de cada uno por 4 para hallar el área del tetraedro (AT):
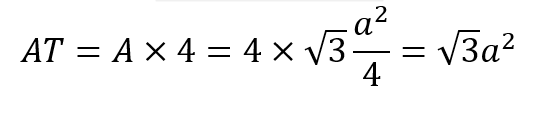
Por otro lado, si queremos calcular el volumen, debemos hallar la altura del poliedro. Para ello, nos guiaremos de la siguiente imagen:
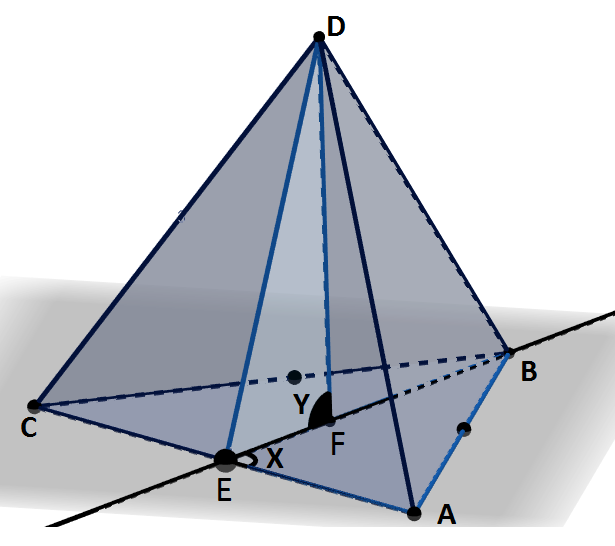
Primero, calcularemos la altura (h) de la base (el triángulo ABC en este ejemplo), que es el segmento EB. El ángulo X mide 90º, por lo que debe cumplirse el teorema de Pitágoras, y la hipotenusa (BA), que mide a (la longitud de todas las aristas en este tetraedro), es igual a la suma de cada cateto elevado al cuadrado. Uno de los catetos es EA, es la mitad del segmento AC (E corta el lado en dos partes iguales) y mide a/2. Asimismo, el segundo cateto es la altura de la base (h o EB).
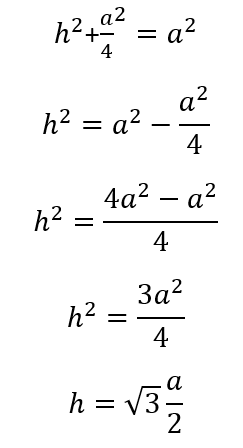
Luego, por propiedad del tetraedro regular, siendo F el centro del triángulo, EF será una tercera parte del segmento EB, es decir, un tercio de h.
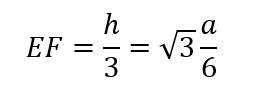
Paso siguiente, para hallar la altura del tetraedro (DF), podemos volver a aplicar el teorema de Pitágoras porque, al ser la altura perpendicular, el ángulo Y es recto (mide 90º).
Viendo el triángulo DEF, la hipotenusa es DE, que es la altura del triángulo ADC y, como todas las caras son iguales, es la misma altura h del triángulo ABC. A su vez, un cateto es la altura del tetraedro (DF), que llamaremos ht, y el otro cateto es el segmento EF que ya lo calculamos. Por lo tanto:
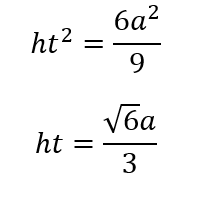
Finalmente, para hallar el volumen del tetraedro (V), como explicamos previamente, multiplicamos la altura de la figura (ht) por el área de la base (A) que está calculada arriba, y lo dividimos entre tres:
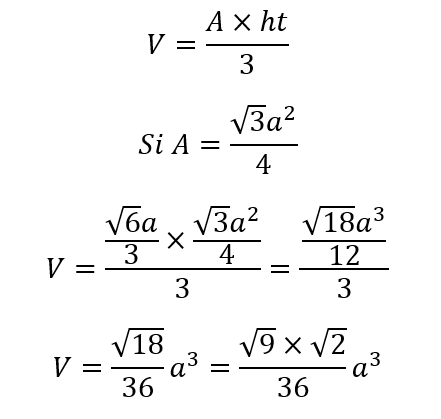
Ejemplo de tetraedro
Suponiendo que un tetraedro es regular y cada lado de sus caras mide 20 metros. ¿Cuál es el área (AT) y volumen (V) de la figura?
